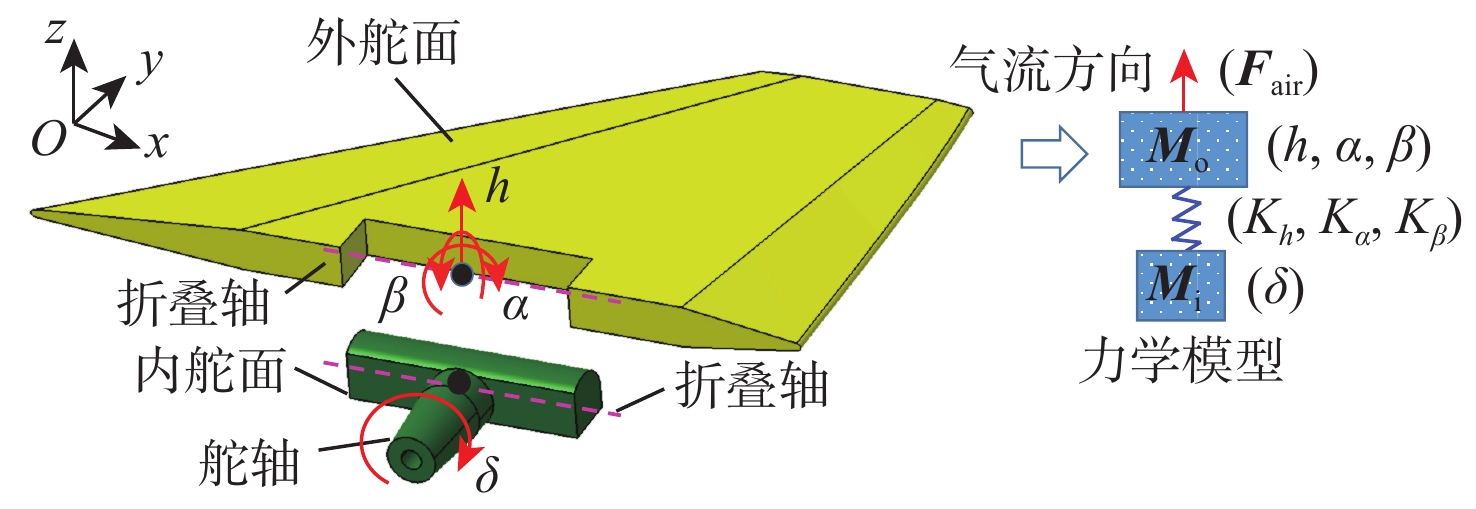
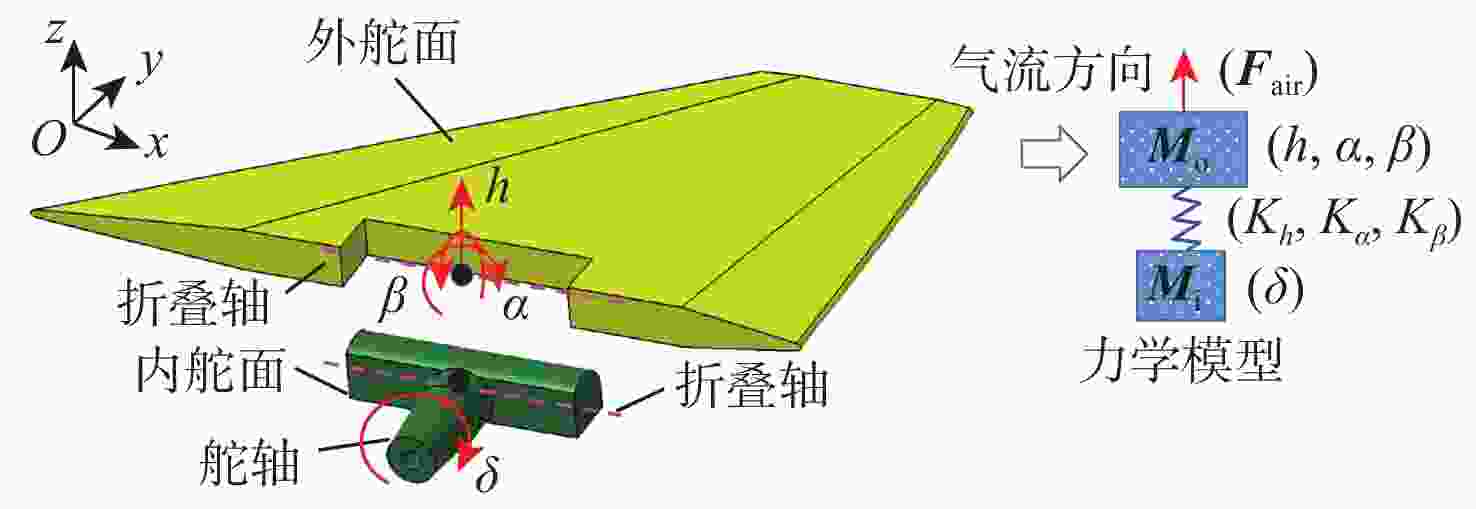
Flutter suppression method for multi-freepalys folding fin based on sliding mode control and fin shaft drive
-
摘要:
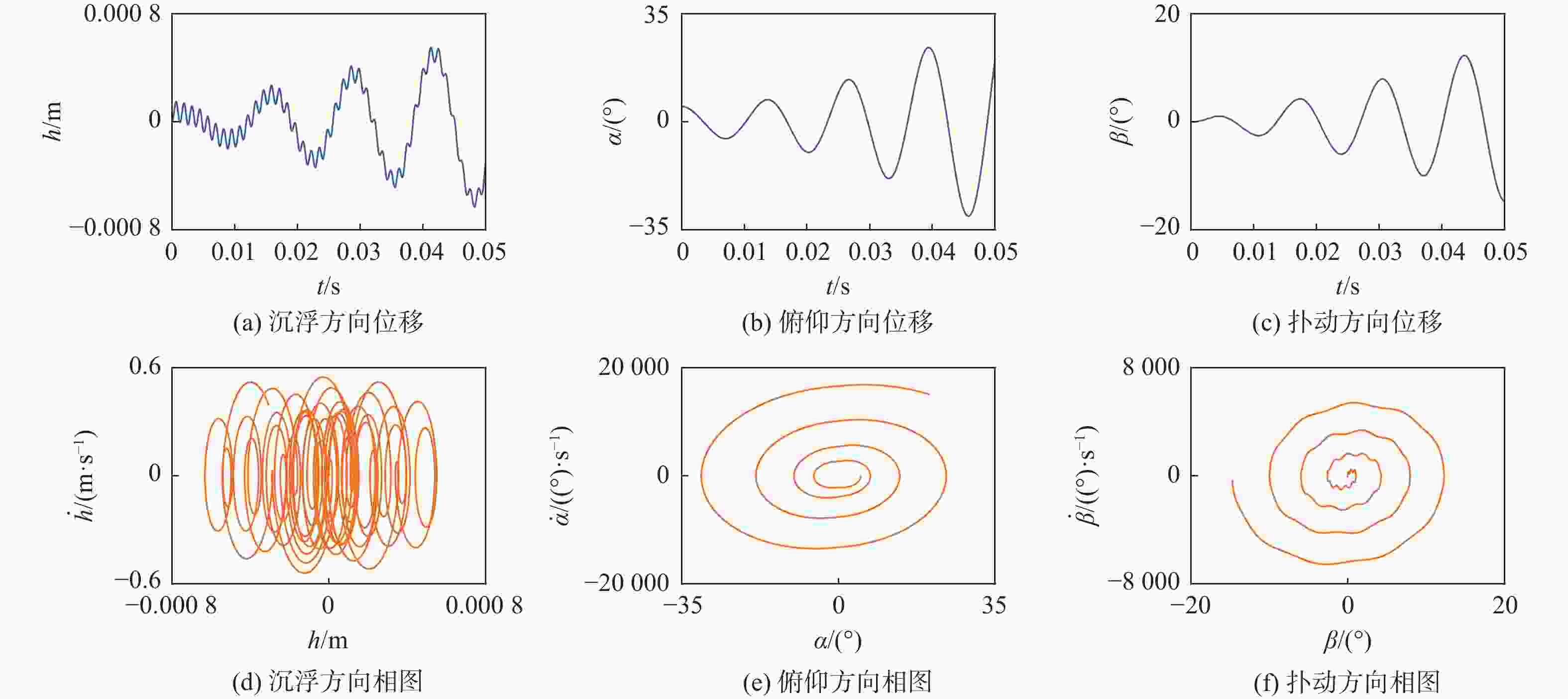
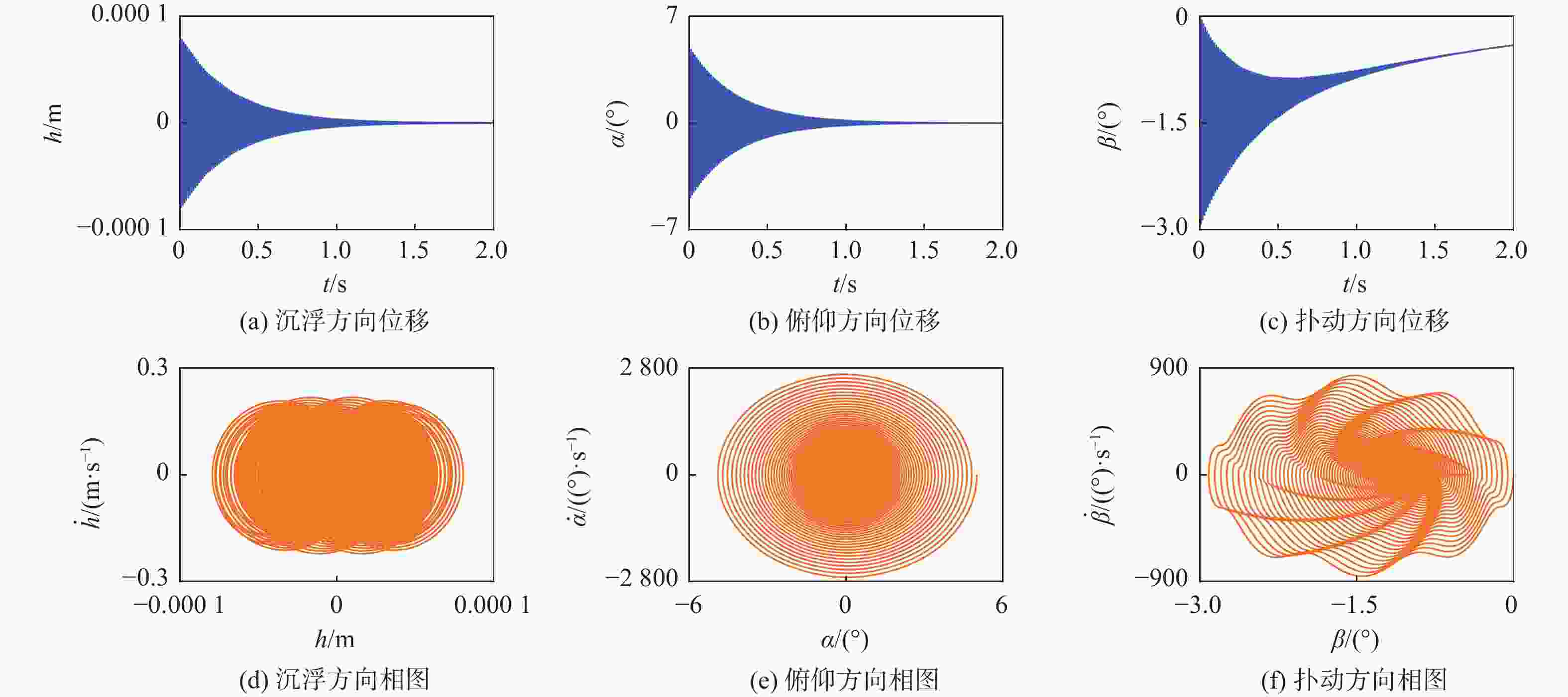
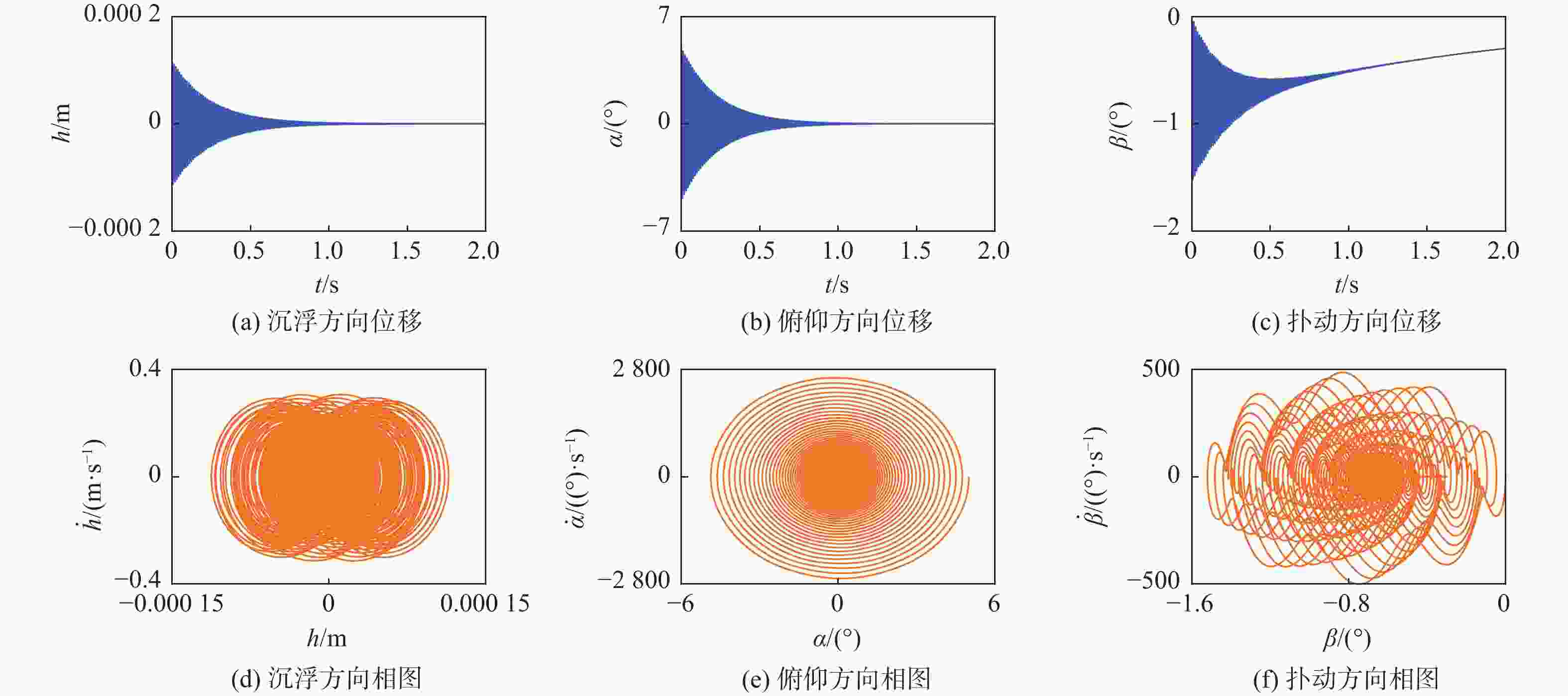
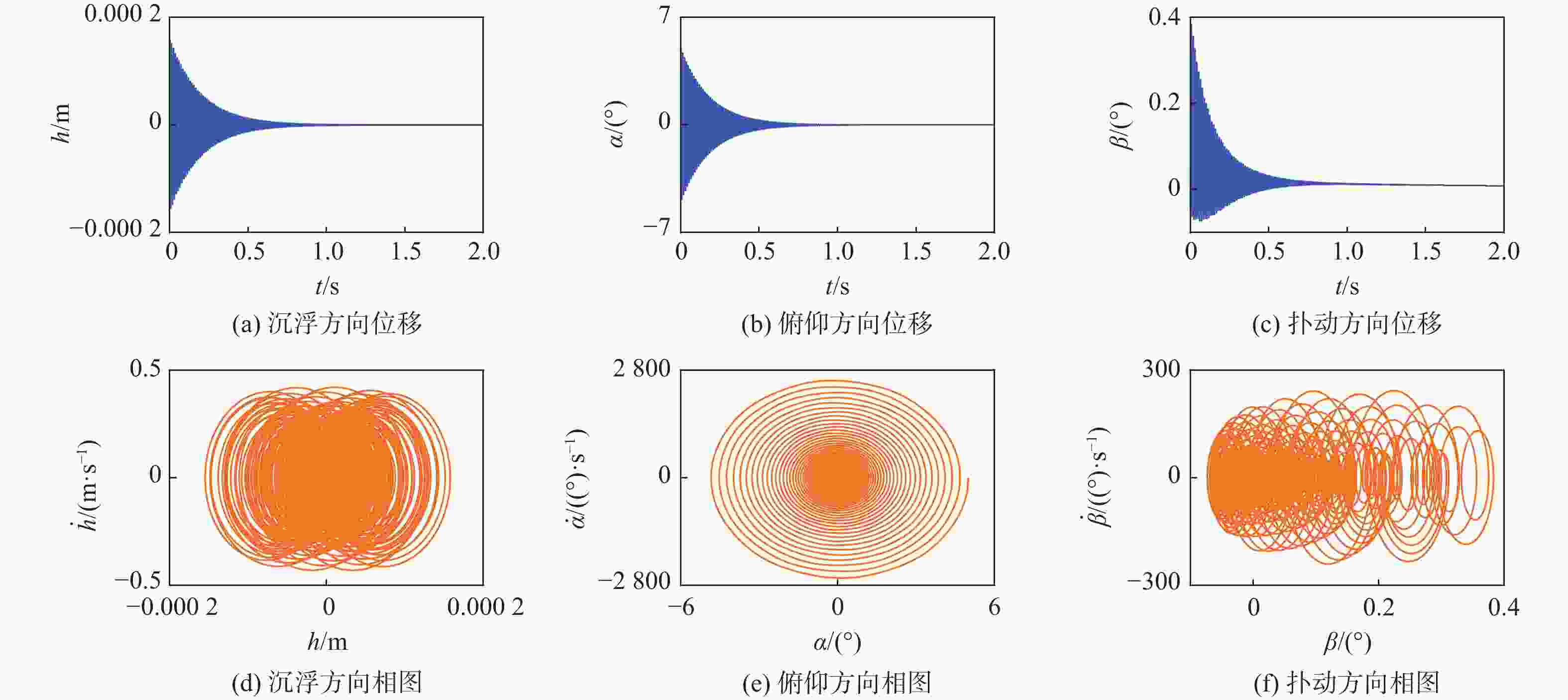
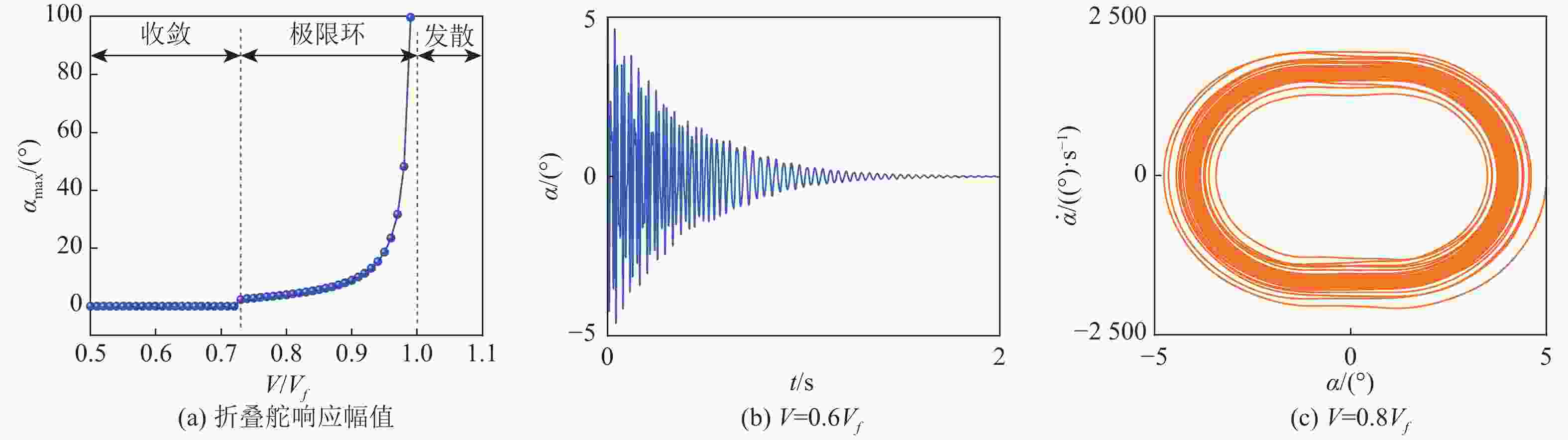
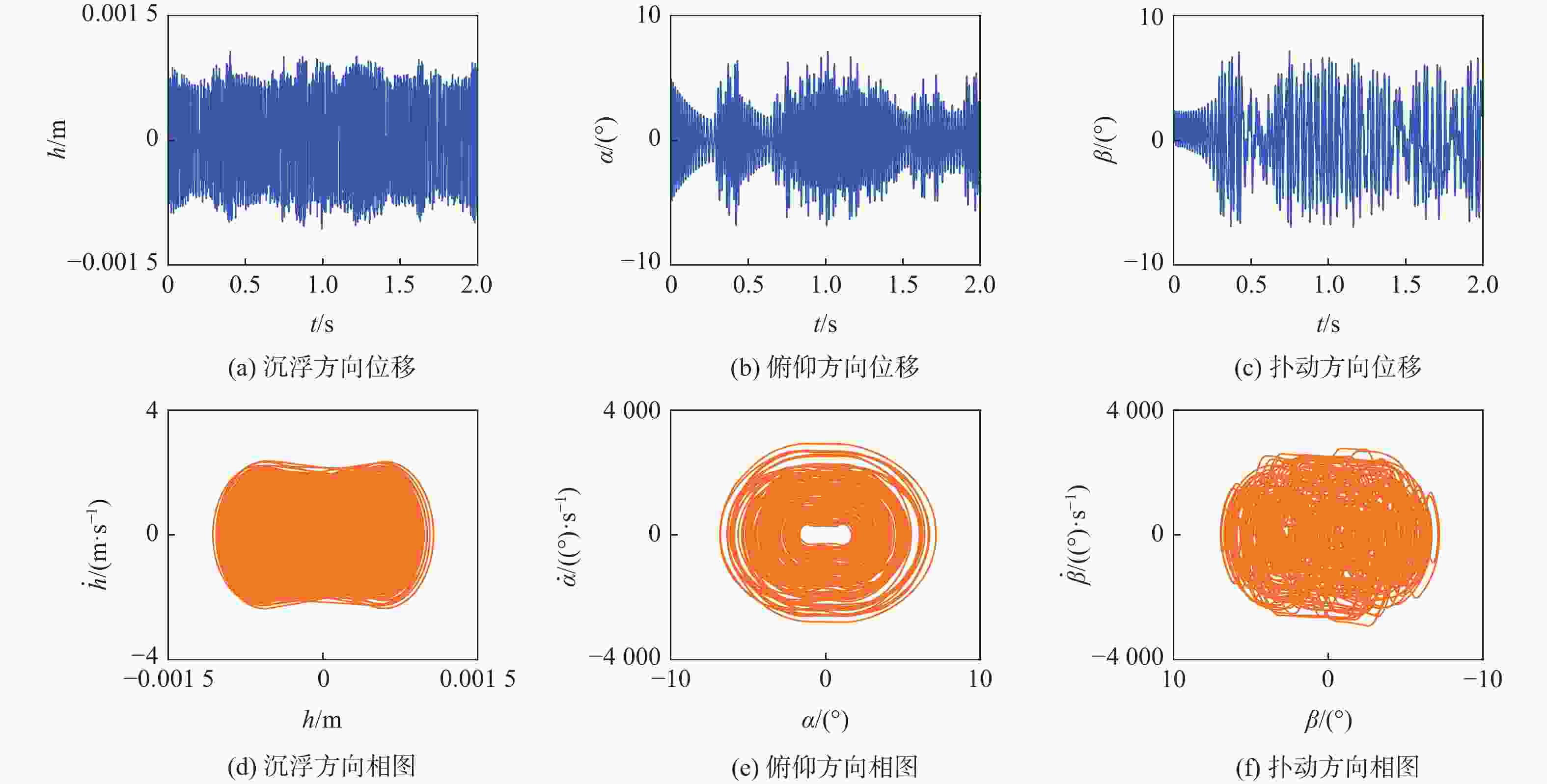
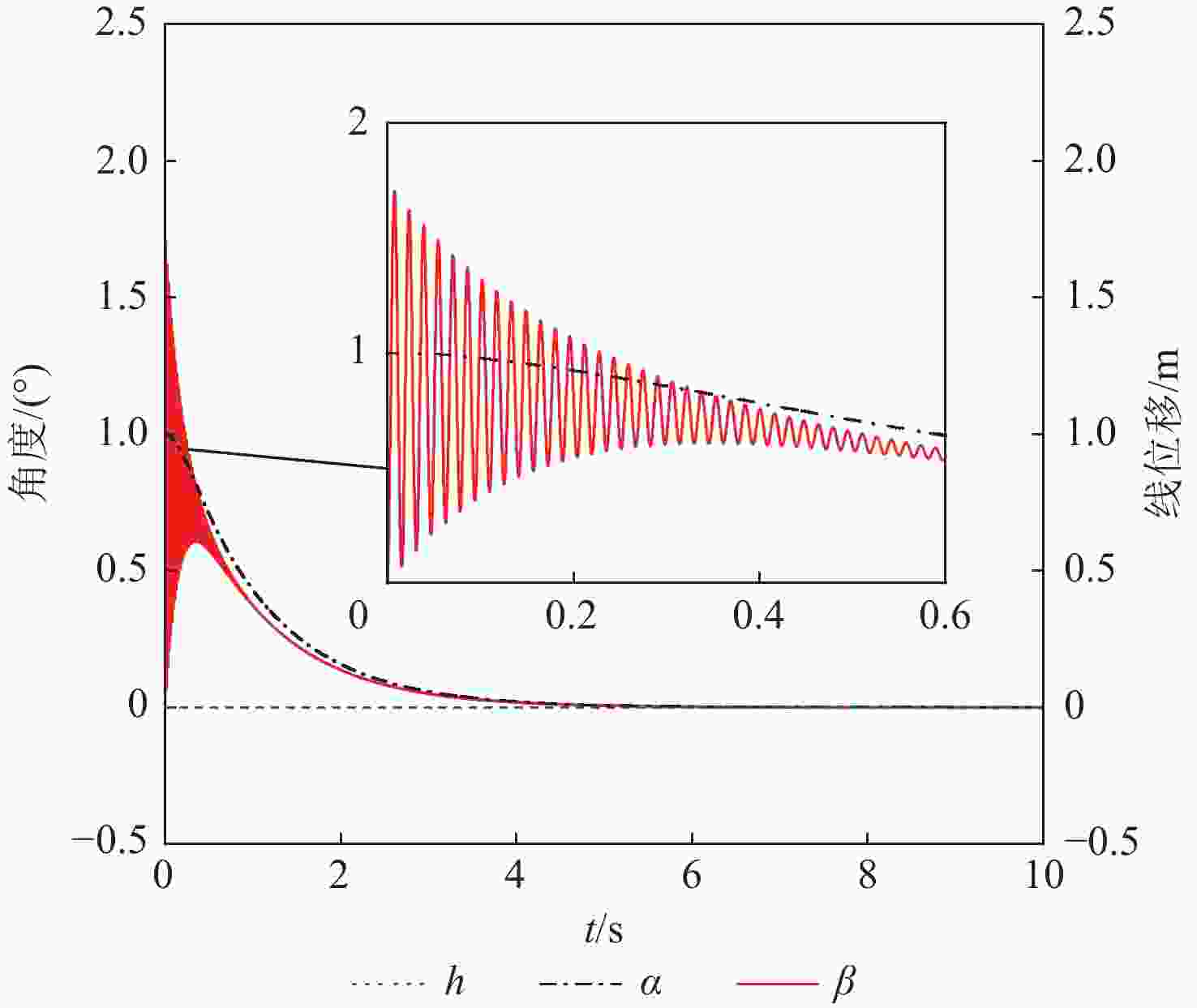
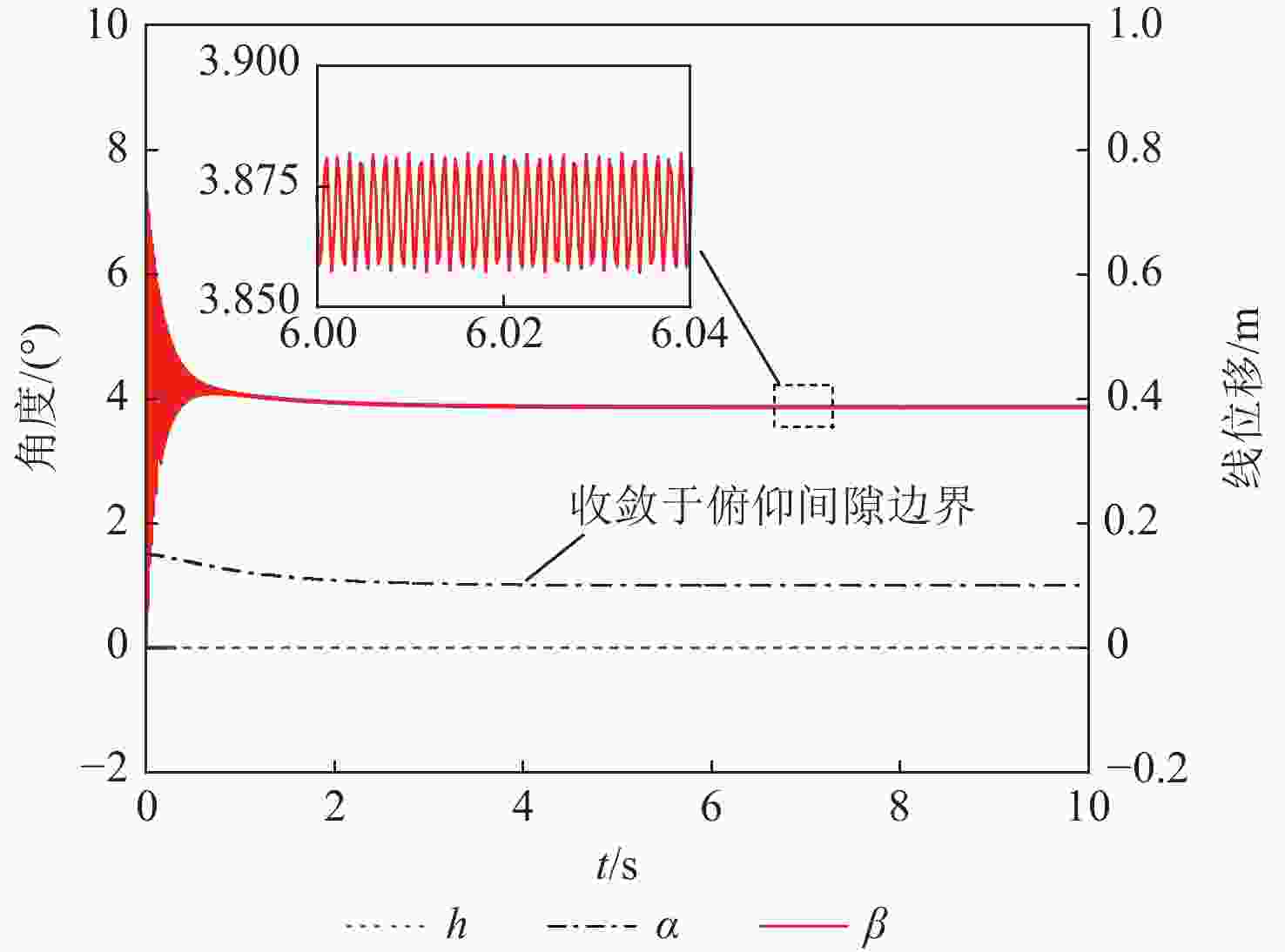
高速飞行器折叠舵因连接结构存在间隙，在飞行过程中易出现非线性动力学行为，气动弹性主动抑制技术是重要的解决方案。由于全动折叠舵只有内舵的舵轴转动位移是输入参数，基于滑模控制网络，提出通过控制舵轴转动来实现多间隙折叠舵颤振主动抑制的新方法。基于三维折叠舵模型和活塞理论非定常气动力计算方法，采用线性弹簧模型描述内/外舵折叠机构连接刚度，推导了四自由度折叠舵动力学模型，阐述了舵轴驱动对线性折叠舵系统颤振抑制的可行性和控制机理；进一步将折叠机构连接刚度模型改为间隙非线性弹簧，分析了多间隙非线性折叠舵气动弹性响应行为和滑模控制的颤振抑制效果。研究结果表明：对于所分析的折叠舵系统，沉浮间隙和扑动间隙有利于提高颤振速度，而俯仰间隙将降低颤振速度；采用滑模控制方法能够有效提高线性和间隙非线性折叠舵面的颤振速度。所提方法和结果为新型折叠舵系统的设计和气动弹性控制提供了一种工程化解决思路。
Abstract:The folding fin of a high-speed vehicle demonstrates nonlinear dynamic behavior during flight due to freeplays in the connection structure, and the aeroelastic active suppression technology is an important solution. Because the axis rotation displacement of the inner fin is the only input parameter for the full-motion folding fin, a new method is proposed to realize the active flutter suppression of multi-gap folding fin, by controlling the rotation of the rudder axis based on the sliding mode control. Firstly, based on the three-dimensional folding fin model and the piston theory aerodynamic method, the linear spring model is used to describe the connection stiffness of the folding mechanism, and a four-degree-of-freedom folding fin dynamic model is derived. The feasibility and control mechanism of the fin shaft drive for the flutter suppression of linear folding fin system are illustrated. Further, the connection stiffness model of the folding mechanism is changed to the clearance nonlinear spring, and the behavior of the multi-clearance nonlinear folding fin aeroelasticity response is analyzed. The flutter suppression effect of multi-clearance nonlinear folding rudder is analyzed. The results show that: for the folding fin in this paper, the plunging and flapping clearances increase the flutter speed, while the pitching clearances reduce the flutter speed; the sliding mode control can effectively improve the flutter speed of linear and clearance nonlinear folding fin. The methods and results of this paper provide an engineering solution for the design and aeroelastic control of the folding fin system.
-
Key words:
- folding fin /
- free-play /
- aeroelasticity /
- sliding mode control /
- flutter suppression /
- nonlinear vibration
-
图 4 0.6Vf时含沉浮间隙折叠舵的时域响应和相图
Figure 4. Time histories and phase plane diagram and of folding fin with plunging free-play at 0.6Vf
图 5 0.8Vf时含沉浮间隙折叠舵的时域响应和相图
Figure 5. Time histories and phase plane diagram and of folding fin with plunging free-play at 0.8Vf
图 6 Vf时含沉浮间隙折叠舵的时域响应和相图
Figure 6. Time histories and phase plane diagram and of folding fin with plunging free-play at Vf
图 7 0.6Vf时含俯仰间隙折叠舵的时域响应和相图
Figure 7. Time histories and phase plane diagram and of folding fin with pitching free-play at 0.6Vf
图 8 0.8Vf时含俯仰间隙折叠舵的时域响应和相图
Figure 8. Time histories and phase plane diagram and of folding fin with pitching free-play at 0.8Vf
图 9 Vf时含俯仰间隙折叠舵的时域响应和相图
Figure 9. Time histories and phase plane diagram and of folding fin with pitching free-play at Vf
图 10 0.6Vf时含扑动间隙折叠舵的时域响应和相图
Figure 10. Time histories and phase plane diagram and of folding fin with flapping free-play at 0.6Vf
图 11 0.8Vf时含扑动间隙折叠舵的时域响应和相图
Figure 11. Time histories and phase plane diagram and of folding fin with flapping free-play at 0.8Vf
图 12 Vf时含扑动间隙折叠舵的时域响应和相图
Figure 12. Time histories and phase plane diagram and of folding fin with flapping free-play at Vf
图 13 含俯仰间隙折叠舵响应幅值随气流速度变化曲线
Figure 13. Amplitude response versus airflow velocity of folding fin with pitch free-play
图 14 Vf时含三间隙折叠舵的时域响应和相图
Figure 14. Time histories and phase plane diagram and of folding fin with three free-plays at Vf
图 15 Vf条件下被控线性折叠舵系统的位移响应
Figure 15. Displacement response of controlled linear folding fin system at Vf
图 16 Vf条件下线性折叠舵系统控制量u随时间变化
Figure 16. Control parameter u of linear folding fin system versus time at Vf
图 17 Vf条件下线性折叠舵系统滑模函数s随时间变化
Figure 17. Sliding mode function s of linear folding fin system versus time at Vf
图 18 Vf条件下被控间隙折叠舵系统的位移响应
Figure 18. Displacement response of controlled free-paly folding fin system at Vf
图 19 Vf条件下间隙折叠舵系统控制量u随时间变化
Figure 19. Control parameter u of free-paly folding fin system versus time at Vf
图 20 Vf条件下间隙折叠舵系统滑模函数s随时间变化
Figure 20. Sliding mode function s of free-paly folding fin system versus time at Vf
表 1 折叠舵模型的主要参数
Table 1. Main parameters of folding fin model
参数 数值 内舵相对坐标原点绕y轴转动惯量Iyyin/（kg·m2） 0.0039 外舵的质量mout/kg 13.60 外舵质心位置的x坐标${\bar x_{{\text{out}}}}$/m 0.0471 外舵质心位置的y坐标${\bar y_{{\text{out}}}}$/m 0.112 外舵相对坐标原点绕x轴转动惯量Ixxout/（kg·m2） 0.2467 外舵相对坐标原点绕y轴转动惯量Iyyout/（kg·m2） 0.2205 外舵相对坐标原点xy惯量积Ixyout/（kg·m2） 0.1154 折叠机构沉浮线弹簧连接刚度Kh/（N·m−1） 1×108 折叠机构俯仰扭簧连接刚度Kα/（(N·m)·rad−1） 5×104 折叠机构扑动扭簧连接刚度Kβ/（(N·m)·rad−1） 4×104 
下载: 导出CSV
表 2 折叠舵模态频率的本文方法与Nastran结果
Table 2. The proposed method and Nastran results of modal frequency of folding fin
模态阶数 模态频率/Hz 误差/% 振型 本文方法 Nastran结果 一阶 56.028 55.978 0.0893 舵面弯曲 二阶 99.162 99.223 − 0.0615 舵面扭转 三阶 787.853 786.24 0.2052 舵面扑动
下载: 导出CSV
表 3 折叠舵颤振速度和颤振频率的本文方法与Nastran结果
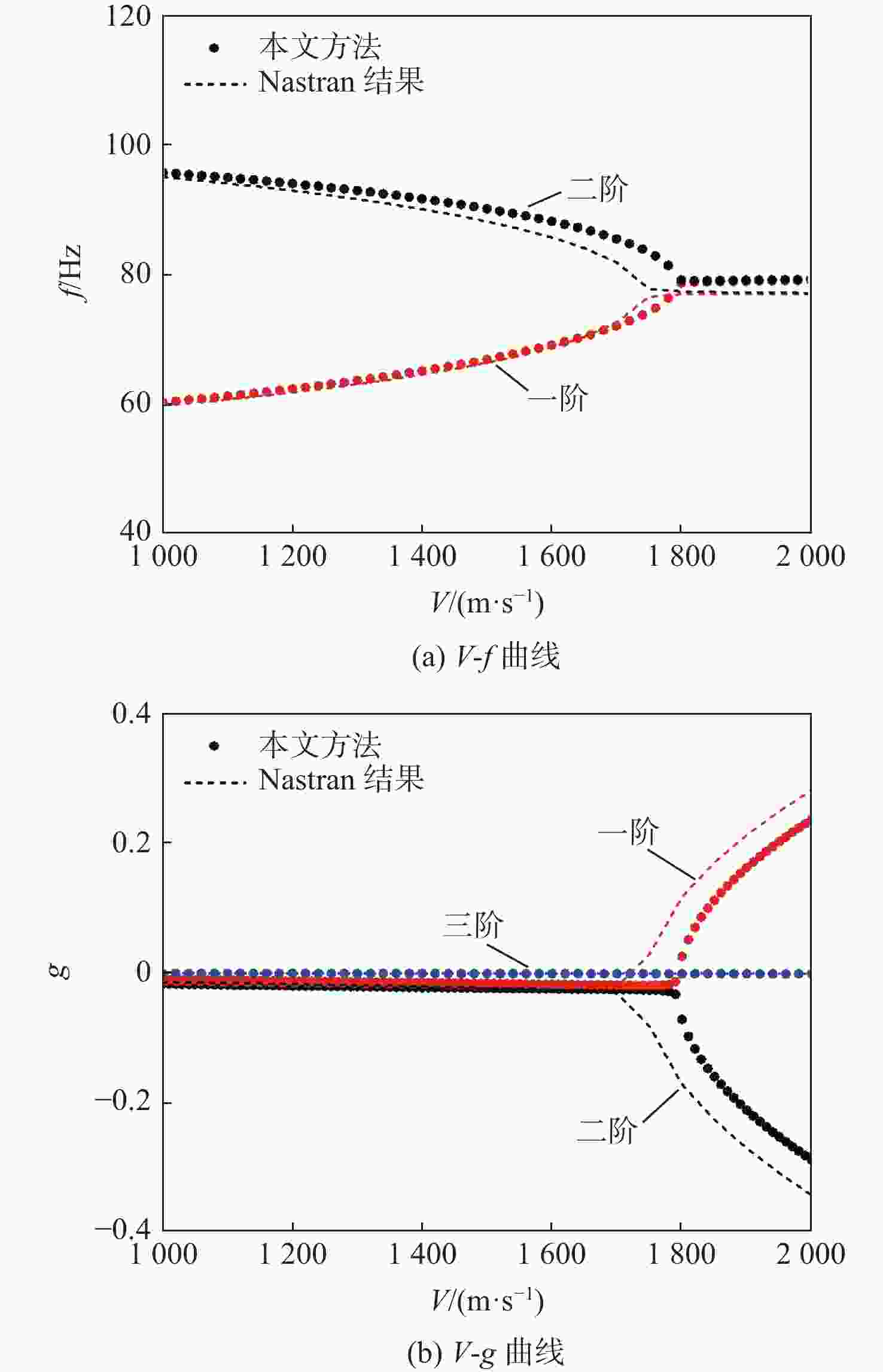
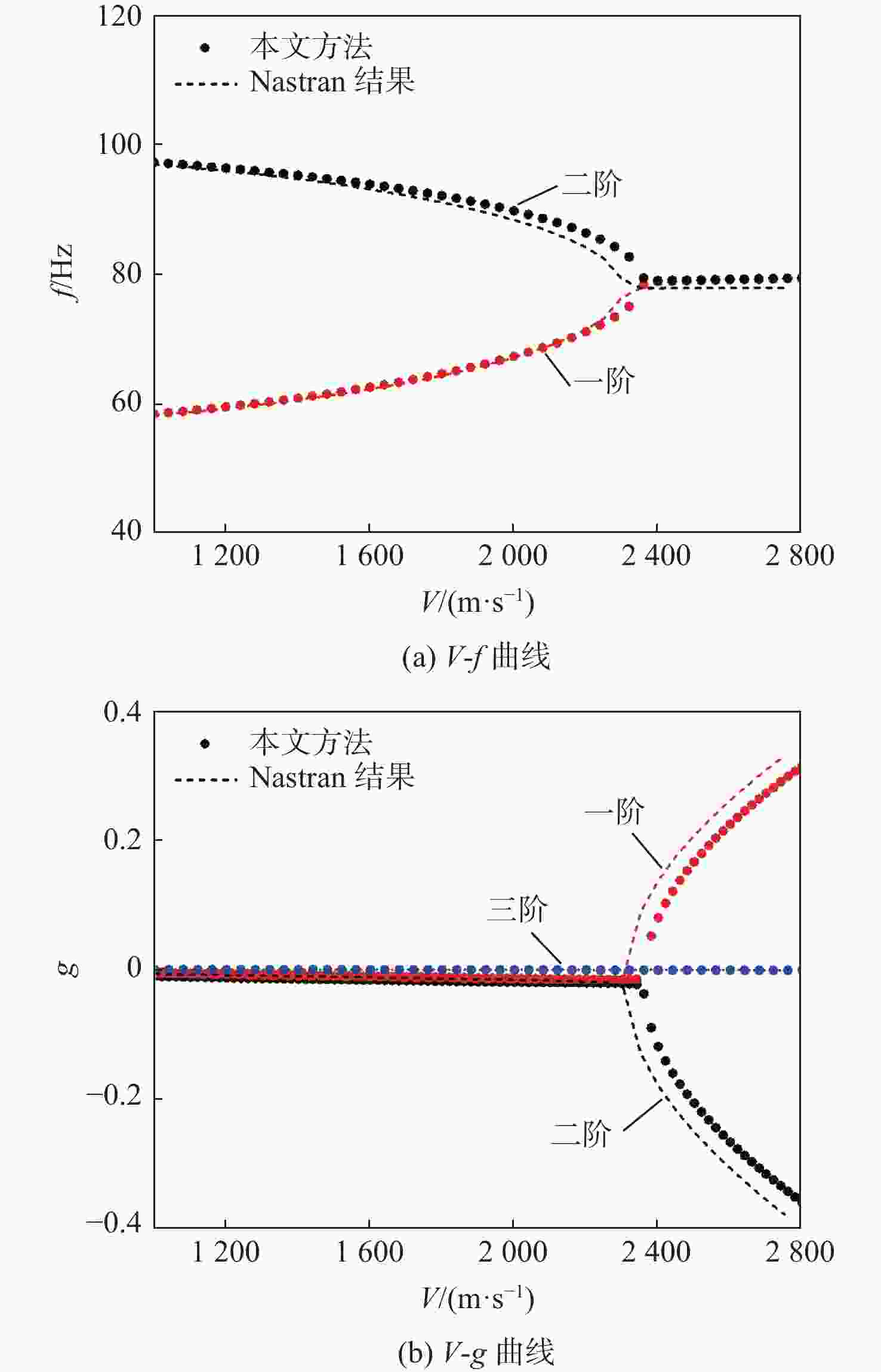
Table 3. The proposed method and Nastran results of flutter speed and frequency for folding fin
Ma 颤振速度/(m·s−1) 频率误差/% 颤振频率/Hz 频率误差/% 本文方法 Nastran 本文方法 Nastran 3 1795 1720 −4.178 79.34 76.63 −3.416 5 2370 2308 −2.616 78.75 77.84 −1.156
下载: 导出CSV
-
[1] SAYLER K M. Emergency military technologies: background and issues for congress: R46458[R]. Washington, D. C. : Congressional Research Service, 2022: 1-37. [2] DIAMANTE R G. Wing fold mechanism: US10272988[P]. 2019-04-30. [3] FOX S J, SAKURAI S, MUNSEN V A. Wing folding system: EP2730499A2[P]. 2014-05-14. [4] 任浩源, 王毅, 王亮, 等. 航天飞行器折叠翼锁紧机构力学模型[J]. 航空动力学报, 2023, 38(12): 3009-3019.REN H Y, WANG Y, WANG L, et al. Mechanical model of locking mechanisms of folding wing for spacecraft[J]. Journal of Aerospace Power, 2023, 38(12): 3009-3019(in Chinese). [5] 陈克, 金玲, 徐倩, 等. 基于高温合金的高速飞行器折叠舵结构设计与研究[J]. 航空兵器, 2022, 29(6): 71-77. doi: 10.12132/ISSN.1673-5048.2022.0024CHEN K, JIN L, XU Q, et al. Design and research of high-speed aircraft folding rudder structure based on high-temperature alloy[J]. Aero Weaponry, 2022, 29(6): 71-77(in Chinese). doi: 10.12132/ISSN.1673-5048.2022.0024 [6] 陈克, 金玲, 雷豹, 等. 高速飞行器折叠翼/舵设计技术与进展研究[J]. 强度与环境, 2022, 49(1): 53-59.CHEN K, JIN L, LEI B, et al. Research on design technology and progress of high-speed aircraft folding wing/rudder[J]. Structure & Environment Engineering, 2022, 49(1): 53-59(in Chinese). [7] LIU S S, ZHAO R, YU K P, et al. Nonlinear system identification framework of folding fins with freeplay using backbone curves[J]. Chinese Journal of Aeronautics, 2022, 35(10): 183-194. doi: 10.1016/j.cja.2022.05.011 [8] HE H N, TANG H, YU K P, et al. Nonlinear aeroelastic analysis of the folding fin with freeplay under thermal environment[J]. Chinese Journal of Aeronautics, 2020, 33(9): 2357-2371. doi: 10.1016/j.cja.2020.05.005 [9] 何昊南, 于开平, 唐宏, 等. 有间隙折叠舵面的振动实验与非线性建模研究[J]. 力学学报, 2019, 51(5): 1476-1488. doi: 10.6052/0459-1879-19-119HE H N, YU K P, TANG H, et al. Vibration experiment and nonlinear modelling research on the folding fin with freeplay[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(5): 1476-1488(in Chinese). doi: 10.6052/0459-1879-19-119 [10] YANG N, WANG N, ZHANG X, et al. Nonlinear flutter wind tunnel test and numerical analysis of folding fins with freeplay nonlinearities[J]. Chinese Journal of Aeronautics, 2016, 29(1): 144-159. doi: 10.1016/j.cja.2015.12.011 [11] ZHOU X H, HUANG R. Subcritical and supercritical nonlinear aeroelastic behavior of a morphing wing with bilinear hinge stiffness[J]. Communications in Nonlinear Science and Numerical Simulation, 2021, 103: 105946. doi: 10.1016/j.cnsns.2021.105946 [12] CASTRICHINI A, HODIGERE SIDDARAMAIAH V, CALDERON D E, et al. Nonlinear folding wing tips for gust loads alleviation[J]. Journal of Aircraft, 2016, 53(5): 1391-1399. doi: 10.2514/1.C033474 [13] FIROUZ-ABADI R D, ALAVI S M. Effect of thickness and angle-of-attack on the aeroelastic stability of supersonic fins[J]. The Aeronautical Journal, 2012, 116(1182): 777-792. doi: 10.1017/S0001924000007272 [14] FIROUZ-ABADI R D, ALAVI S M, SALARIEH H. Analysis of non-linear aeroelastic response of a supersonic thick fin with plunging, pinching and flapping free-plays[J]. Journal of Fluids and Structures, 2013, 40: 163-184. doi: 10.1016/j.jfluidstructs.2013.03.019 [15] RICCI S, TOFFOL F, DE GASPARI A, et al. Wind tunnel system for active flutter suppression research: overview and insights[J]. AIAA Journal, 2022, 60(12): 6692-6714. doi: 10.2514/1.J061985 [16] THEIS J, PFIFER H, SEILER P. Robust modal damping control for active flutter suppression[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(6): 1056-1068. doi: 10.2514/1.G004846 [17] TANG W, WANG Y, GU J W, et al. LPV modeling and controller design for body freedom flutter suppression subject to actuator saturation[J]. Chinese Journal of Aeronautics, 2020, 33(10): 2679-2693. doi: 10.1016/j.cja.2020.05.027 [18] 杨智春, 田玮, 谷迎松, 等. 带集中非线性的机翼气动弹性问题研究进展[J]. 航空学报, 2016, 37(7): 2013-2044. doi: 10.7527/S1000-6893.2016.0140YANG Z C, TIAN W, GU Y S, et al. Advance in the study on wing aeroelasticity with concentrated nonlinearity[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2013-2044(in Chinese). doi: 10.7527/S1000-6893.2016.0140 [19] 黄锐, 胡海岩. 飞行器非线性气动伺服弹性力学[J]. 力学进展, 2021, 51(3): 428-466. doi: 10.6052/1000-0992-21-010HUANG R, HU H Y. Nonlinear aeroservoelasticity of aircraft[J]. Advances in Mechanics, 2021, 51(3): 428-466(in Chinese). doi: 10.6052/1000-0992-21-010 [20] 白刘月, 吴志刚, 杨超. 含间隙全动舵面的非线性颤振模式及被动抑制方法[J]. 北京麻豆精品秘 国产传媒学报, 2023, 49(9): 2361-2373.BAI L Y, WU Z G, YANG C. Nonlinear flutter modes and flutter suppression of an all-movable fin with freeplay[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(9): 2361-2373(in Chinese). [21] EUGENI M, SALTARI F, MASTRODDI F, et al. Structural damping models for passive aeroelastic control[J]. Aerospace Science and Technology, 2021, 118: 107011. doi: 10.1016/j.ast.2021.107011 [22] 宋晨, 王诗其, 杨超. 基于滑模观测器的机翼颤振主动抑制设计[J]. 北京麻豆精品秘 国产传媒学报, 2017, 43(6): 1098-1104.SONG C, WANG S Q, YANG C. Active flutter suppression design of a wing based on sliding mode observer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(6): 1098-1104(in Chinese). [23] OUYANG Y, GU Y S, KOU X P, et al. Active flutter suppression of wing with morphing flap[J]. Aerospace Science and Technology, 2021, 110: 106457. doi: 10.1016/j.ast.2020.106457 [24] 贾尚帅, 丁千. 含间隙超音速二元弹翼非线性颤振与主动控制[J]. 中国科学: 物理学 力学 天文学, 2013, 43(4): 390-400.JIA S S, DING Q. Nonlinear flutter and active control of the supersonic two-dimensional missile wings with a freeplay[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2013, 43(4): 390-400(in Chinese). -
下载:
点击查看大图
计量
- 文章访问数: 217
- HTML全文浏览量: 65
- PDF下载量: 27
- 被引次数: 0
