Scheduling optimization for continuous climb and descend operations in busy terminal area
-
摘要:
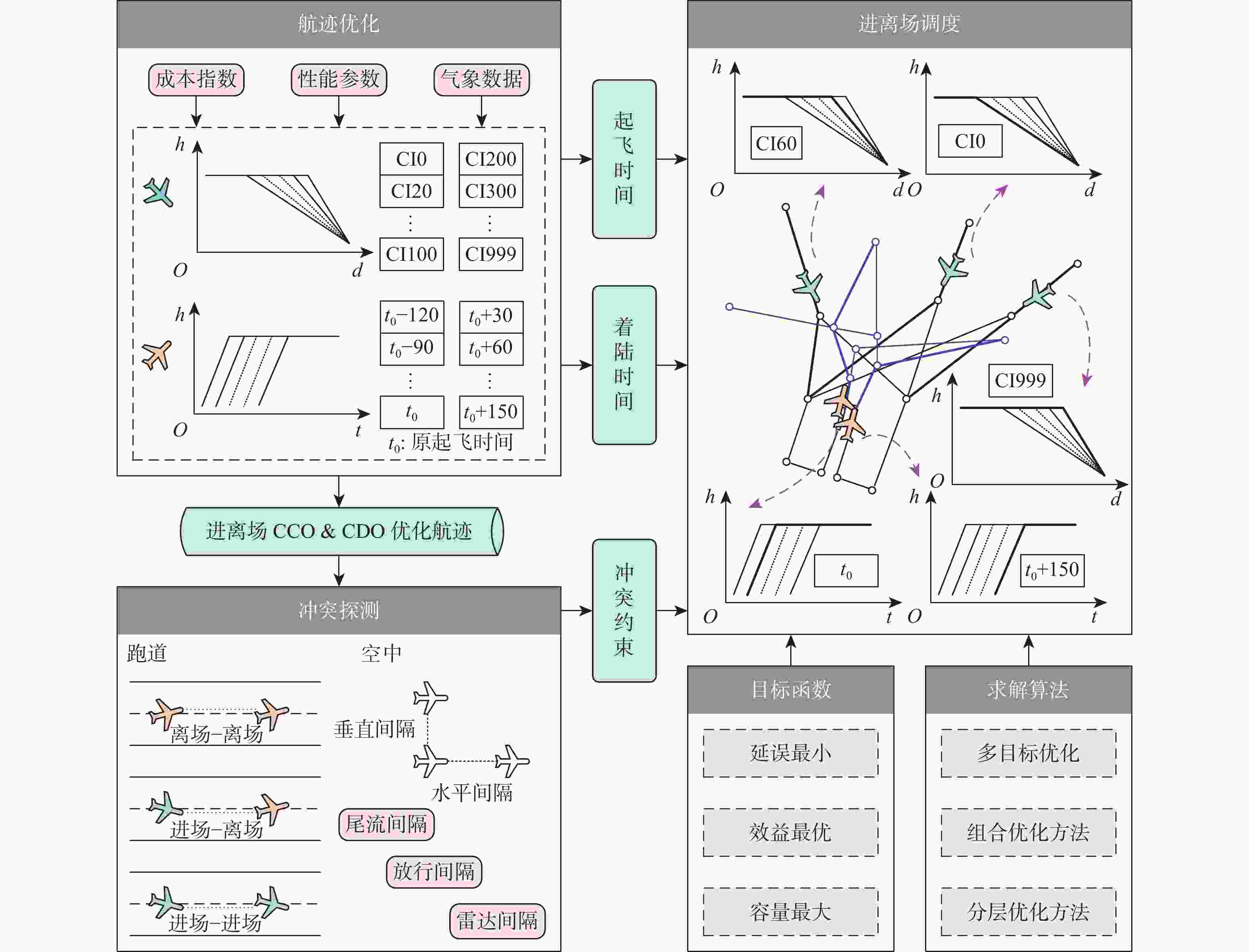
基于现行终端空域结构，提出了一种融合航迹优化、冲突探测与多目标优化的进离场航空器调度方法，助力繁忙终端空域实施连续爬升与下降运行。基于多阶段最优控制理论，采用高斯伪谱法，提出了连续爬升与下降运行的垂直剖面优化方法，实现了基于成本指数的连续爬升与下降运行的航迹优化。依据跑道使用的尾流间隔与放行间隔、空中运行的水平与垂直间隔，采用马氏距离建立了航空器冲突探测模型。考虑空管、航司、机场等运行单位的诉求，提出了优化结果可达的进离场航空器多目标调度模型和方法。选取繁忙时段广州白云国际机场两组进离场数据，设置多种间隔参数，引入备选路径，开展实例分析与对比研究。结果表明：在离场占优的繁忙时段，广州白云国际机场终端空域能够实现繁忙时段下的连续爬升与下降运行；在进场占优的繁忙时段，出现2架航空器无法调度的情况，引入备选路径的方法可以减少无法调度航空器的数量。
Abstract:Based on the current terminal airspace structure, a novel scheduling method for arrival and departure aircraft based on trajectory optimization, conflict detection, and multi-objective optimization is proposed to assist in continuous climb and descent operations in busy terminal airspace. Firstly, a vertical profile optimization method for continuous climb and descent operations is proposed based on multi-stage optimal control theory and the Gaussian pseudo-spectral method, achieving trajectory optimization for continuous climb and descent operations by cost index. Secondly, according to the wake separation and clearance separation used by the runway operations and the horizontal and vertical separation of air operations, an aircraft conflict detection model is established using Mahalanobis distance. Subsequently, considering the demands of operational units such as air traffic control, airlines, and airports, a multi-objective scheduling model and method with achievable optimization results were proposed for arrival and departure aircraft. Finally, two sets of arrival and departure data from Guangzhou Baiyun Airport during peak hours were selected, multiple interval parameters were set, alternative paths were designed, and case analysis and comparative research were conducted. The results indicate that during peak departure hours, the terminal airspace of Guangzhou Baiyun Airport can achieve continuous climb and descent operations during peak hours. Furthermore, during peak arrival hours, two aircraft cannot be scheduled. Introducing alternative paths can reduce the number of aircraft that cannot be scheduled.
-
图 1 连续爬升与下降运行调度优化方法的框架示意
Figure 1. Schematic diagram of the scheduling optimization method for the continuous climb and descent operation
图 4 飞行时间与燃油消耗随成本指数的变化
Figure 4. Variation of flight time and fuel consumption with different cost index
图 5 进离场调度与进场调度延误分布对比
Figure 5. Variation of flight time and fuel consumption with different cost index
图 7 不同优化方法对应的跑道使用分布
Figure 7. Distribution of runway use with different optimization methods
表 1 参数设置
Table 1. Parameters setting table
参数
组合离场偏离/
min跑道运行间隔 空中运行间隔 离场/s 进场/s 进离/s 垂直/m 水平/km 1 [−4:1:5] 90 120 120 300 6 2 [−4:1:5] 90 150 150 400* 10* 3 [−2:0.5:2.5] 90 120 120 300 6 4 [−2: 0.5:2.5] 90 150 150 400 10 注：*垂直间隔400 m与水平间隔10 km为本文仿真设置的比实际运行更严格的间隔标准。 
下载: 导出CSV
表 2 进场调度与进离场调度结果对比
Table 2. Arrival scheduling versus arrival and departure scheduling results
s 调度
类型平均进场
延误平均离场
偏离最大飞行
时间平均飞行
时间进场 15.5 1 359.0 1 120.0 进离场 53.5 47.7 1 407.0 1 158.0
下载: 导出CSV
表 3 多目标优化的权重系数与优先级
Table 3. Weights & priorities of multi-objective optimization
优化
方案最小化平均
进场延误式（3）最小化平均
离场偏离式（4）最小化最大进场
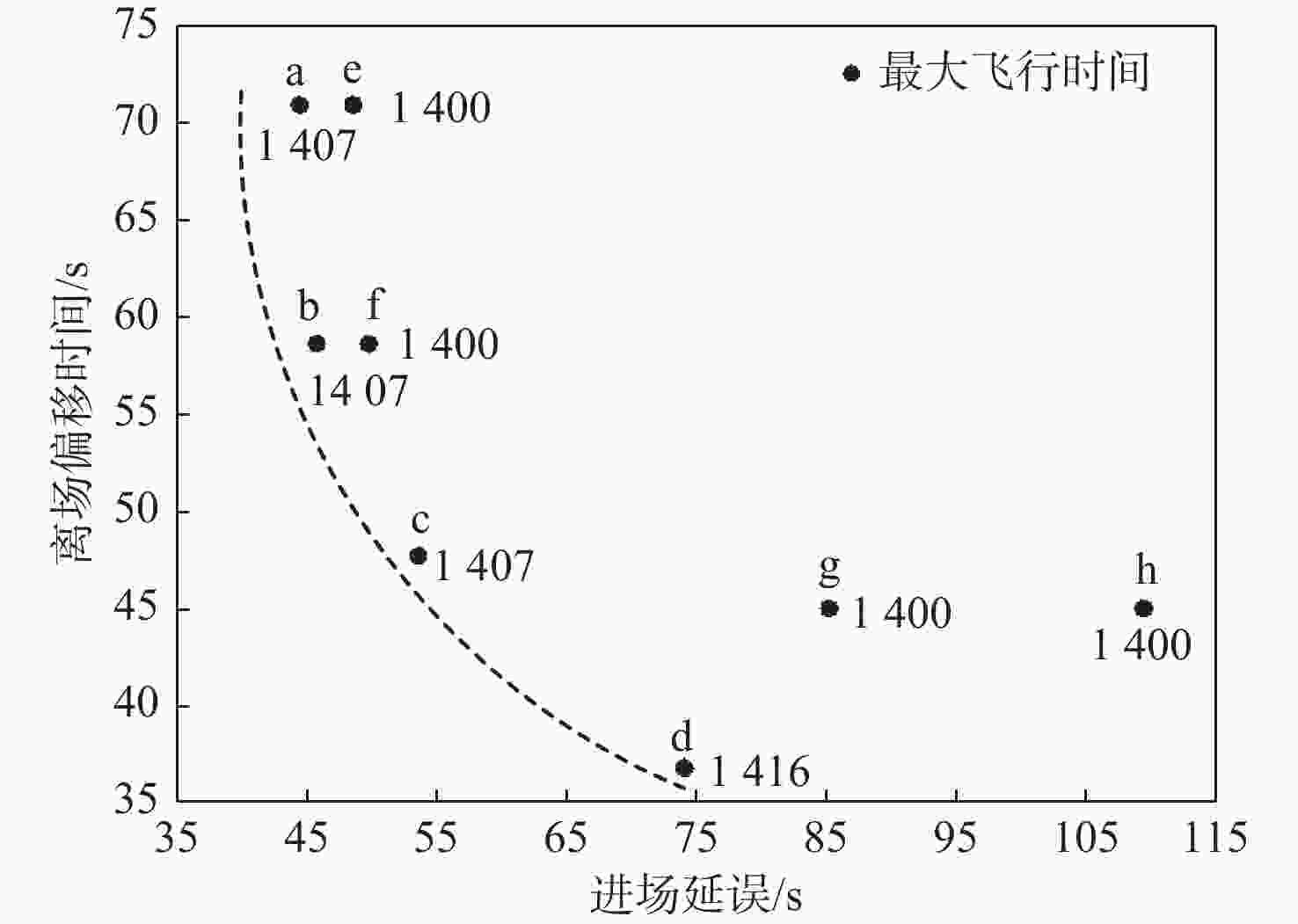
飞行时间式（5）权重 优先级 权重 优先级 权重 优先级 a 首先 其次 b 2.0 1.0 c 1.0 1.0 d 1.0 2.0 e 其次 再次 首先 f 1.0 1.0 首先 g 再次 其次 首先 h 其次 首先
下载: 导出CSV
表 4 进场调度与进离场调度结果对比
Table 4. Arrival scheduling versus arrival and departure scheduling results
s 参数
组合平均进场
延误平均离场
偏离最大飞行
时间平均飞行
时间1 53.5 47.7 1 407.0 1 158.0 2 115.6 100.9 1 512.0 1 220.1 3 65.1 27.3 1 462.0 1 169.6 4 110.9 64.1 1 512.0 1 211.3
下载: 导出CSV
表 5 路径变化的进场调度与进离场调度结果对比
Table 5. Arrival scheduling versus arrival and departure scheduling results under the change of arrival routes
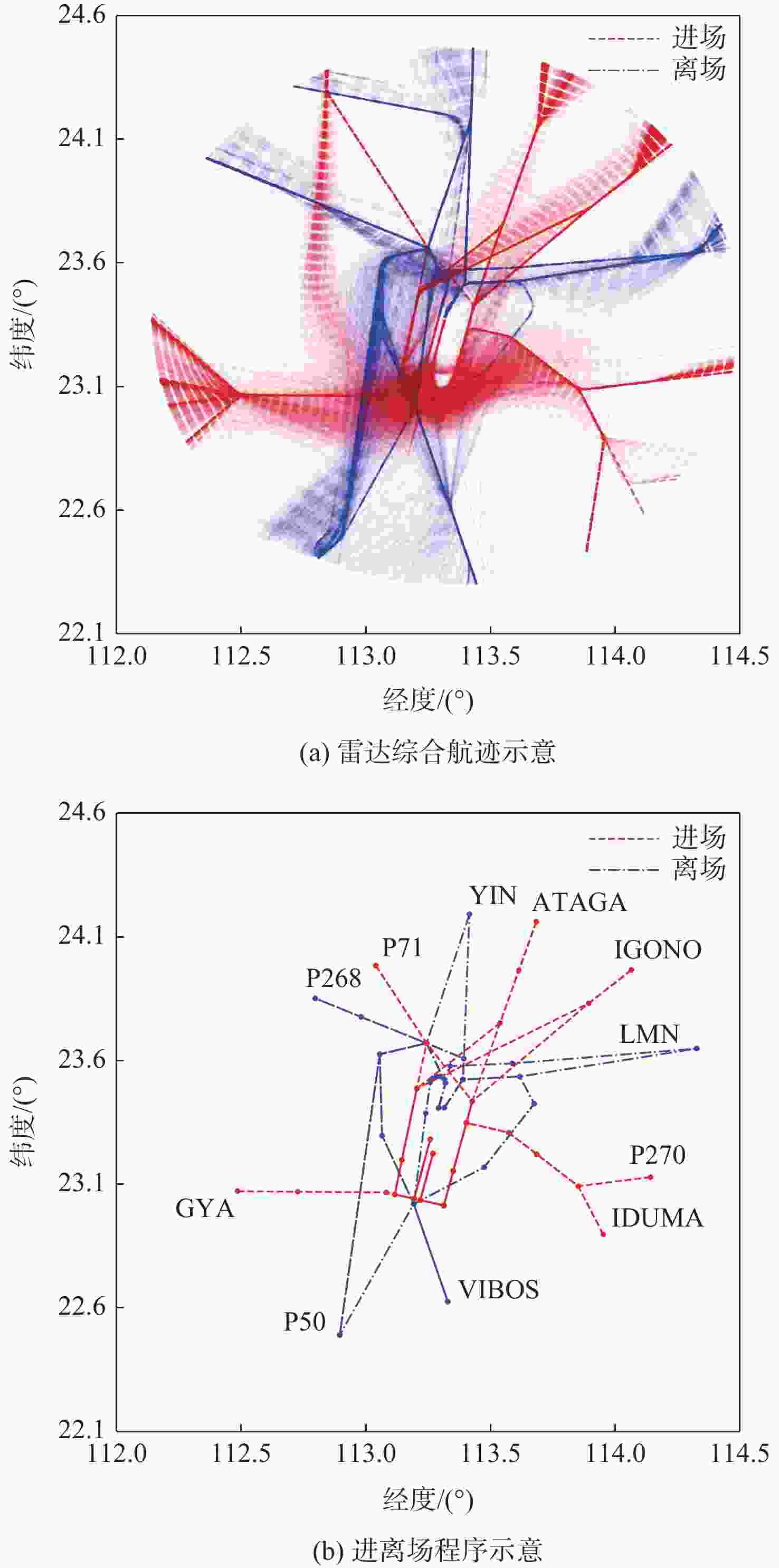
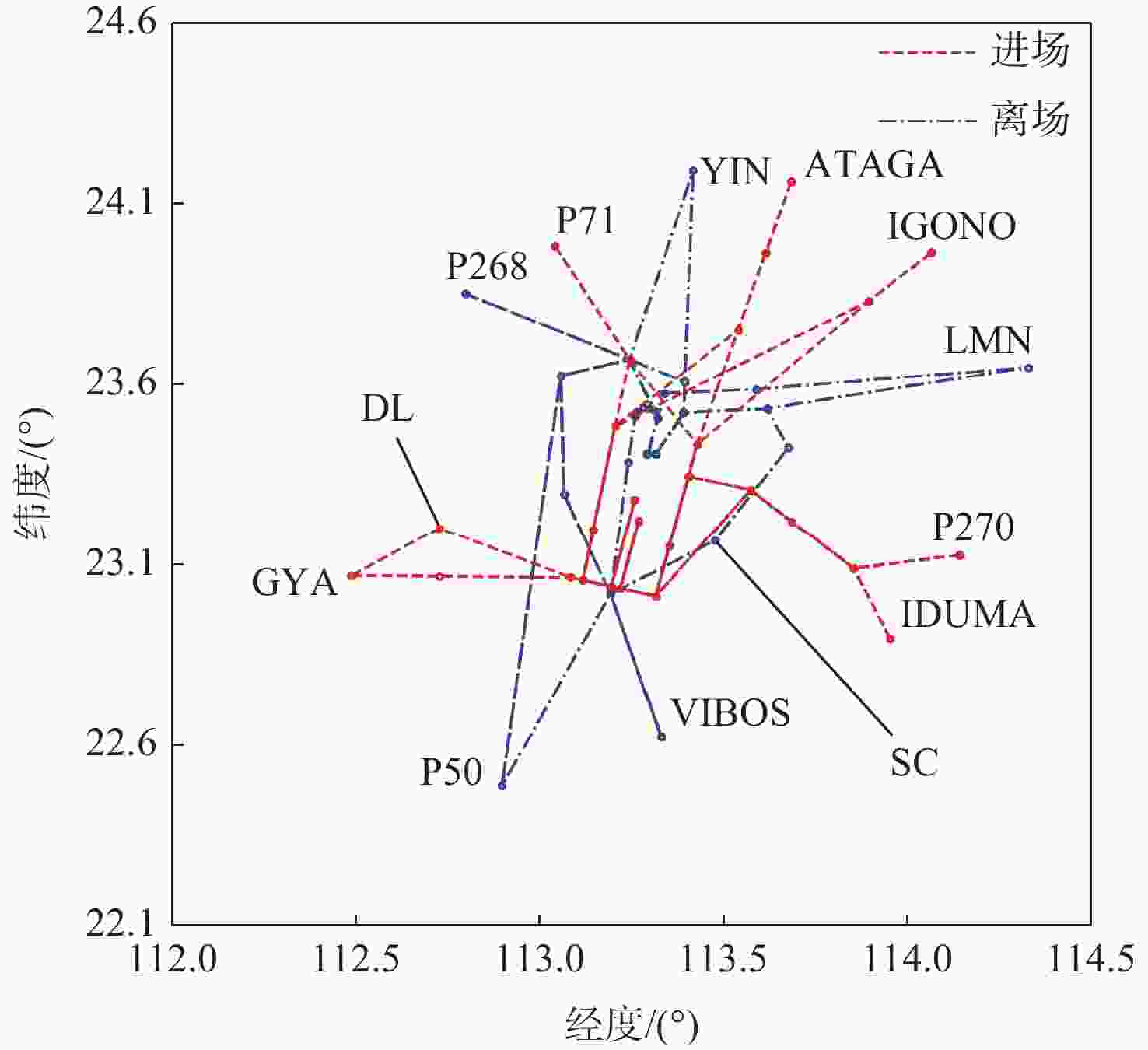
参数组合 进场路径 平均进场延误/s 平均离场偏离/s 最大飞行时间/s 平均飞行时间/s 无法调度/架 1 STAR 66.8 21.8 1 512.0 1 200.9 2 2 STAR 67.7 40.0 1 444.0 1 203.9 7 1 GYA-DL 86.3 21.8 1 549.0 1 223.9 0 2 GYA-DL 112.6 36.4 1 602.0 1 241.5 5 2 GYA-DL
IDUMA-SC117.3 36.4 1 602.0 1 241.5 5
下载: 导出CSV
-
[1] LIU J, ZHANG J F, DAI X M, et al. Research on trajectory generation and optimization in continuous descent operations[C]//Proceedings of the 2018 Aviation Technology, Integration, and Operations Conference. AIAA, 2018: 2018-3986. [2] JIN L, CAO Y, SUN D F. Investigation of potential fuel savings due to continuous-descent approach[J]. Journal of Aircraft, 2013, 50(3): 807-816. doi: 10.2514/1.C032000 [3] DALMAU R. Optimal trajectory management for aircraft descent operations subject to time constraints[D]. Barcelona: Technical University of Catalonia, 2019: 5-6. [4] 张军峰, 游录宝, 杨春苇, 等. 基于多目标帝国竞争算法的进场排序与调度[J]. 航空学报, 2021, 42(6): 324439.ZHANG J F, YOU L B, YANG C W, et al. Arrival sequencing and scheduling based on multi-objective Imperialist competitive algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(6): 324439(in Chinese). [5] LIANG M, DELAHAYE D, MARECHAL P. Conflict-free arrival and departure trajectory planning for parallel runway with advanced point-merge system[J]. Transportation Research Part C: Emerging Technologies, 2018, 95: 207-227. doi: 10.1016/j.trc.2018.07.006 [6] 杨磊, 李文博, 刘芳子, 等. 柔性空域结构下连续下降航迹多目标优化[J]. 航空学报, 2021, 42(2): 324157.YANG L, LI W B, LIU F Z, et al. Multi-objective optimization of continuous descending trajectories in flexible airspace[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(2): 324157(in Chinese). [7] HU R, FENG H L, WITLOX F, et al. Airport capacity constraints and air traffic demand in China[J]. Journal of Air Transport Management, 2022, 103: 102251. doi: 10.1016/j.jairtraman.2022.102251 [8] SÁEZ R, PRATS X, POLISHCHUK T, et al. Traffic synchronization in terminal airspace to enable continuous descent operations in trombone sequencing and merging procedures: An implementation study for Frankfurt airport[J]. Transportation Research Part C: Emerging Technologies, 2020, 121: 102875. doi: 10.1016/j.trc.2020.102875 [9] SÁEZ R, POLISHCHUK T, SCHMIDT C, et al. Automated sequencing and merging with dynamic aircraft arrival routes and speed management for continuous descent operations[J]. Transportation Research Part C: Emerging Technologies, 2021, 132: 103402. doi: 10.1016/j.trc.2021.103402 [10] GUI D D, LE M L, HUANG Z C, et al. Optimal aircraft arrival scheduling with continuous descent operations in busy terminal maneuvering areas[J]. Journal of Air Transport Management, 2023, 107: 102344. doi: 10.1016/j.jairtraman.2022.102344 [11] HONG Y, CHOI B, LEE K, et al. Dynamic robust sequencing and scheduling under uncertainty for the point merge system in terminal airspace[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(9): 2933-2943. doi: 10.1109/TITS.2017.2766683 [12] KAMO S, ROSENOW J, FRICKE H, et al. Robust optimization integrating aircraft trajectory and sequence under weather forecast uncertainty[J]. Transportation Research Part C: Emerging Technologies, 2023, 152: 104187. doi: 10.1016/j.trc.2023.104187 [13] TORATANI D, WICKRAMASINGHE N K, WESTPHAL J, et al. Feasibility study on applying continuous descent operations in congested airspace with speed control functionality: fixed flight-path angle descent[J]. Aerospace Science and Technology, 2020, 107: 106236. doi: 10.1016/j.ast.2020.106236 [14] LIEDER A, BRISKORN D, STOLLETZ R. A dynamic programming approach for the aircraft landing problem with aircraft classes[J]. European Journal of Operational Research, 2015, 243(1): 61-69. doi: 10.1016/j.ejor.2014.11.027 [15] 张军峰, 游录宝, 周铭, 等. 基于点融合系统的多目标进场排序与调度[J]. 北京麻豆精品秘 国产传媒学报, 2023, 49(1): 66-73.ZHANG J F, YOU L B, ZHOU M, et al. Multi-objective arrival sequencing and scheduling based on point merge system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(1): 66-73(in Chinese). [16] BENNELL J A, MESGARPOUR M, POTTS C N. Airport runway scheduling[J]. Annals of Operations Research, 2013, 204(1): 249-270. doi: 10.1007/s10479-012-1268-1 [17] IKLI S, MANCEL C, MONGEAU M, et al. The aircraft runway scheduling problem: a survey[J]. Computers & Operations Research, 2021, 132: 105336. [18] BENNELL J A, MESGARPOUR M, POTTS C N. Dynamic scheduling of aircraft landings[J]. European Journal of Operational Research, 2017, 258(1): 315-327. doi: 10.1016/j.ejor.2016.08.015 [19] SAMÀ M, D’ARIANO A, D’ARIANO P, et al. Scheduling models for optimal aircraft traffic control at busy airports: tardiness, priorities, equity and violations considerations[J]. Omega, 2017, 67: 81-98. doi: 10.1016/j.omega.2016.04.003 [20] YANG Y C, GAO Z C, HE C. Stochastic terminal flight arrival and departure scheduling problem under performance-based navigation environment[J]. Transportation Research Part C: Emerging Technologies, 2020, 119: 102735. doi: 10.1016/j.trc.2020.102735 [21] DU Z M, ZHANG J F, KANG B. A data-driven method for arrival sequencing and scheduling problem[J]. Aerospace, 2023, 10(1): 62. doi: 10.3390/aerospace10010062 [22] ZHANG J F, LIU J, HU R, et al. Online four-dimensional trajectory prediction method based on aircraft intent updating[J]. Aerospace Science and Technology, 2018, 77: 774-787. doi: 10.1016/j.ast.2018.03.037 [23] RAO A V, BENSON D A, DARBY C, et al. Algorithm 902: GPOPS, a MATLAB software for solving multiple-phase optimal control problems using the Gauss Pseudo-spectral method[J]. ACM Transactions on Mathematical Software, 2010, 37(2): 1-39. [24] GILL P E, WONG E, MURRAY W, et al. User's guide for SNOPT version 7.5: software for large-scale nonlinear programming[R]. San Diego: University of California, 2015. [25] GUI X H, ZHANG J F, TANG X M, et al. A data-driven trajectory optimization framework for terminal maneuvering area operations[J]. Aerospace Science and Technology, 2022, 131(1): 108010. [26] ZHANG J F, ZHAO P L, ZHANG Y, et al. Criteria selection and multi-objective optimization of aircraft landing problem[J]. Journal of Air Transport Management, 2020, 82: 101734. doi: 10.1016/j.jairtraman.2019.101734 -
下载:
点击查看大图
计量
- 文章访问数: 393
- HTML全文浏览量: 104
- PDF下载量: 17
- 被引次数: 0
