Cover selection method for batch image steganography based on multivariate optimization
-
摘要:
批量图像隐写通过载体选择在多张载体图像中嵌入秘密信息,为社交网络中的隐蔽通信提供有效的途径。与传统的图像隐写相比,批量图像隐写的关键科学问题是在保证抗检测性能的情况下设计有效的载体选择方法。基于此,提出一种基于多元优化的批量图像隐写载体选择方法,通过联合分析嵌入失真、图像相关性、嵌入容量三元因素,将批量图像隐写中的载体选择建模为多元优化问题。同时,针对社交网络可能对载密图像进行压缩的情况,在批量图像隐写载体选择时设计了秘密信息分片与重组策略,提升了批量图像隐写的鲁棒性。充分的实验结果表明:所提方法在抗检测性能、嵌入容量和鲁棒性上取得了令人满意的效果,为基于社交网络的隐蔽通信提供了技术支撑。
Abstract:Batch image steganography provides an effective means for covert communication on social networks by embedding secret messages into multiple cover images through cover selection. Compared with traditional image steganography, a key challenge of batch image steganography lies in designing an effective cover selection method while ensuring good undetectability performance. In this paper, a multivariate optimization-based cover selection method for batch image steganography was proposed. By jointly analyzing embedding distortion, image correlation, and embedding capacity, this method modelled the cover selection for batch image steganography as a multivariate optimization problem. Additionally, to enhance the batch image steganography robustness against the possible compression of images after steganography by social networks, a secret message fragmentation and reassembly strategy was designed. Experimental results demonstrate that the proposed method for batch image steganography achieves satisfactory performance in undetectability, embedding capacity, and robustness, providing technical support for covert communication on social networks.
-
Key words:
- multivariate optimization /
- batch image steganography /
- cover selection /
- undetectability /
- robustness
-
表 1 单因素下的抗检测性分析
Table 1. Undetectability analysis under single-factor conditions
方法 PE k= 1000 k= 2000 k= 3000 k= 4000 k= 5000 Rand 0.2564 0.2266 0.2122 0.2012 0.1974 Dis 0.3410 0.3065 0.2872 0.2679 0.2520 IS 0.3442 0.3049 0.2786 0.2690 0.2520 EC 0.3522 0.3163 0.2900 0.2729 0.2553 表 2 不同条件下的错误检测概率(QF=60)
Table 2. Probability of false detections under different conditions (QF = 60)
嵌入率 特征集 方法 PE k= 1000 k= 2000 k= 3000 k= 4000 k= 5000 0.4 cfstar Rand 0.3058 0.2835 0.2732 0.2600 0.2600 Liao[13] 0.3696 0.3311 0.3095 0.2954 0.2801 Wang[14] 0.3760 0.3478 0.3239 0.3049 0.2989 本文方法 0.3802 0.3482 0.3285 0.3053 0.2966 ccJRM Rand 0.2900 0.2686 0.2585 0.2490 0.2488 Liao[13] 0.3508 0.3253 0.3009 0.2865 0.2677 Wang[14] 0.3598 0.3360 0.3138 0.2985 0.2882 本文方法 0.3630 0.3381 0.3168 0.2989 0.2895 0.5 cfstar Rand 0.2502 0.2203 0.2023 0.1905 0.1885 Liao[13] 0.3115 0.2630 0.2388 0.2241 0.2085 Wang[14] 0.3167 0.2803 0.2540 0.2359 0.2244 本文方法 0.3221 0.2869 0.2557 0.2353 0.2236 ccJRM Rand 0.2298 0.2022 0.1887 0.1747 0.1725 Liao[13] 0.2840 0.2485 0.2300 0.2108 0.1913 Wang[14] 0.2936 0.2640 0.2406 0.2213 0.2022 本文方法 0.2990 0.2675 0.2430 0.2199 0.2055 表 3 不同条件下的错误检测概率(QF=75)
Table 3. Probability of false detections under different conditions (QF = 75)
嵌入率 特征集 方法 PE k= 1000 k= 2000 k= 3000 k= 4000 k= 5000 0.4 cfstar Rand 0.3282 0.3067 0.2971 0.2866 0.2834 Liao[13] 0.4203 0.3879 0.3665 0.3566 0.3373 Wang[14] 0.4307 0.3948 0.3781 0.3632 0.3515 本文方法 0.4275 0.3975 0.3847 0.3648 0.3525 ccJRM Rand 0.3128 0.2875 0.2813 0.2713 0.2689 Liao[13] 0.4002 0.3764 0.3542 0.3364 0.3234 Wang[14] 0.4036 0.3831 0.3639 0.3463 0.3358 本文方法 0.4071 0.3846 0.3655 0.3512 0.3353 0.5 cfstar Rand 0.2800 0.2521 0.2358 0.2220 0.2159 Liao[13] 0.3800 0.3379 0.3127 0.2896 0.2775 Wang[14] 0.3847 0.3474 0.3244 0.3031 0.2826 本文方法 0.3943 0.3485 0.3285 0.3032 0.2890 ccJRM Rand 0.2564 0.2266 0.2122 0.2012 0.1974 Liao[13] 0.3410 0.3065 0.2872 0.2679 0.2520 Wang[14] 0.3510 0.3174 0.2919 0.2754 0.2660 本文方法 0.3533 0.3203 0.2933 0.2777 0.2661 表 4 不同条件下的错误检测概率(QF=90)
Table 4. Probability of false detections under different conditions (QF = 90)
嵌入率 特征集 方法 PE k= 1000 k= 2000 k= 3000 k= 4000 k= 5000 0.4 cfstar Rand 0.3249 0.3132 0.3098 0.3016 0.2994 Liao[13] 0.4013 0.3938 0.3847 0.3810 0.3741 Wang[14] 0.4134 0.4060 0.3963 0.3827 0.3700 本文方法 0.4213 0.4105 0.4047 0.3913 0.3784 ccJRM Rand 0.3168 0.2983 0.2919 0.2871 0.2846 Liao[13] 0.4009 0.3917 0.3778 0.3702 0.3612 Wang[14] 0.4146 0.3956 0.3841 0.3769 0.3620 本文方法 0.4195 0.4004 0.3865 0.3780 0.3639 0.5 cfstar Rand 0.2804 0.2599 0.2521 0.2407 0.2373 Liao[13] 0.3660 0.3576 0.3406 0.3320 0.3175 Wang[14] 0.3758 0.3655 0.3529 0.3326 0.3165 本文方法 0.3824 0.3660 0.3551 0.3355 0.3210 ccJRM Rand 0.2671 0.2469 0.2370 0.2290 0.2277 Liao[13] 0.3648 0.3467 0.3275 0.3182 0.3056 Wang[14] 0.3662 0.3535 0.3396 0.3255 0.3053 本文方法 0.3735 0.3568 0.3396 0.3285 0.3159 表 5 Wang等的方法[14]和本文方法嵌入容量的对比
Table 5. Comparison of embedding capacity between Wang et al.’s method[14] and proposed method
QF 方法 嵌入容量/bit k= 1000 k= 2000 k= 3000 k= 4000 k= 5000 60 Wang[14] 69254497 122784610 168444548 207175886 235671773 本文方法 69264640 122781191 168444548 207293584 235880610 75 Wang[14] 88527118 157237348 216089517 267350520 309605320 本文方法 88540196 157251458 216143376 267350520 309758006 90 Wang[14] 121091974 221886393 310810927 389066645 461304521 本文方法 121203657 222234100 311097664 389620084 462032474 表 6 不同平均数据丢失率下的秘密信息恢复正确率
Table 6. Accuracy of secret information recovery under different average data loss rates
% 数据冗余率 平均数据丢失率 恢复正确率 嵌入率为0.15 嵌入率为0.25 44.44 33.49 72 65 51.72 0 0 83.87 81.27 56 43 91.24 0 0 -
[1] SALMAN A. Facebook by the numbers[EB/OL]. (2022-12-08)[2023-04-13]. http://omnicoreagency.com/-facebook-statistics/. [2] SIMMONS G J. The prisoners’ problem and the subliminal channel[C]//Advances in Cryptology. Berlin: Springer, 1984: 51-67. [3] FILLER T, JUDAS J, FRIDRICH J. Minimizing additive distortion in steganography using syndrome-trellis codes[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(3): 920-935. doi: 10.1109/TIFS.2011.2134094 [4] HOLUB V, FRIDRICH J. Digital image steganography using universal distortion[C]//Proceedings of the First ACM Workshop on Information Hiding and Multimedia Security. New York: ACM, 2013: 59-68. [5] GUO L J, NI J Q, SHI Y Q. Uniform embedding for efficient JPEG steganography[J]. IEEE Transactions on Information Forensics and Security, 2014, 9(5): 814-825. doi: 10.1109/TIFS.2014.2312817 [6] COGRANNE R, GIBOULOT Q, BAS P. Steganography by minimizing statistical detectability: the cases of JPEG and color images[C]//Proceedings of the ACM Workshop on Information Hiding and Multimedia Security. New York: ACM, 2020: 161-167. [7] PAN Y F, NI J Q, SU W K. Improved uniform embedding for efficient JPEG steganography[C]//Cloud Computing and Security. Berlin: Springer, 2016: 125-133. [8] WANG Z C, ZHANG X P, YIN Z X. Hybrid distortion function for JPEG steganography[J]. Journal of Electronic Imaging, 2016, 25: 050501. doi: 10.1117/1.JEI.25.5.050501 [9] WEI Q D, YIN Z X, WANG Z C, et al. Distortion function based on residual blocks for JPEG steganography[J]. Multimedia Tools and Applications, 2018, 77(14): 17875-17888. doi: 10.1007/s11042-017-5053-7 [10] 张卫明, 王宏霞, 李斌, 等. 多媒体隐写研究进展[J]. 中国图象图形学报, 2022, 27(6): 1918-1943. doi: 10.11834/jig.211272ZHANG W M, WANG H X, LI B, et al. Overview of steganography on multimedia[J]. Journal of Image and Graphics, 2022, 27(6): 1918-1943(in Chinese). doi: 10.11834/jig.211272 [11] KER A D. Batch steganography and pooled steganalysis[C]//Information Hiding. Berlin: Springer, 2007: 265-281. [12] KER A D. Perturbation hiding and the batch steganography problem[C]//Information Hiding. Berlin: Springer, 2008: 45-59. [13] LIAO X, YIN J J, CHEN M L, et al. Adaptive payload distribution in multiple images steganography based on image texture features[J]. IEEE Transactions on Dependable and Secure Computing, 2022, 19(2): 897-911. [14] WANG Z C, FENG G R, SHEN L Q, et al. Cover selection for steganography using image similarity[J]. IEEE Transactions on Dependable and Secure Computing, 2023, 20(3): 2328-2340. [15] YIN Z X, KE L F. Robust adaptive steganography based on dither modulation and modification with re-compression[J]. IEEE Transactions on Signal and Information Processing Over Networks, 2021, 7: 336-345. doi: 10.1109/TSIPN.2021.3081373 [16] DUAN X L, LI B, YIN Z X, et al. Robust image steganography against lossy JPEG compression based on embedding domain selection and adaptive error correction[J]. Expert Systems with Applications, 2023, 229: 120416. doi: 10.1016/j.eswa.2023.120416 [17] KER A D. A capacity result for batch steganography[J]. IEEE Signal Processing Letters, 2007, 14(8): 525-528. doi: 10.1109/LSP.2006.891319 [18] EVSUTIN O, KOKURINA A, MESHCHERYAKOV R. Approach to the selection of the best cover image for information embedding in JPEG images based on the principles of the optimality[J]. Journal of Decision Systems, 2018, 27(S1): 256-264. doi: 10.1080/12460125.2018.1460163 [19] ZHONG N, QIAN Z X, WANG Z C, et al. Batch steganography via generative network[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2021, 31(1): 88-97. doi: 10.1109/TCSVT.2020.2974884 [20] WANG Z C, ZHANG X P, QIAN Z X. Practical cover selection for steganography[J]. IEEE Signal Processing Letters, 2019, 27: 71-75. [21] WANG Z C, ZHANG X P, YIN Z X. Joint cover-selection and payload-allocation by steganographic distortion optimization[J]. IEEE Signal Processing Letters, 2018, 25(10): 1530-1534. doi: 10.1109/LSP.2018.2865888 [22] HOLUB V, FRIDRICH J, DENEMARK T. Universal distortion function for steganography in an arbitrary domain[J]. EURASIP Journal on Information Security, 2014, 2014(1): 1. doi: 10.1186/1687-417X-2014-1 [23] KODOVSKY J, FRIDRICH J, HOLUB V. Ensemble classifiers for steganalysis of digital media[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(2): 432-444. doi: 10.1109/TIFS.2011.2175919 [24] KODOVSKÝ J, FRIDRICH J. Steganalysis of JPEG images using rich models[C]//Media Watermarking, Security, and Forensics, Bellingham: SPIE, 2012, 8303: 7. [25] JESSICA F. BOSSbase[EB/OL]. (2018-10-23)[2023-04-13]. http://dde.binghamton.edu/download/. -






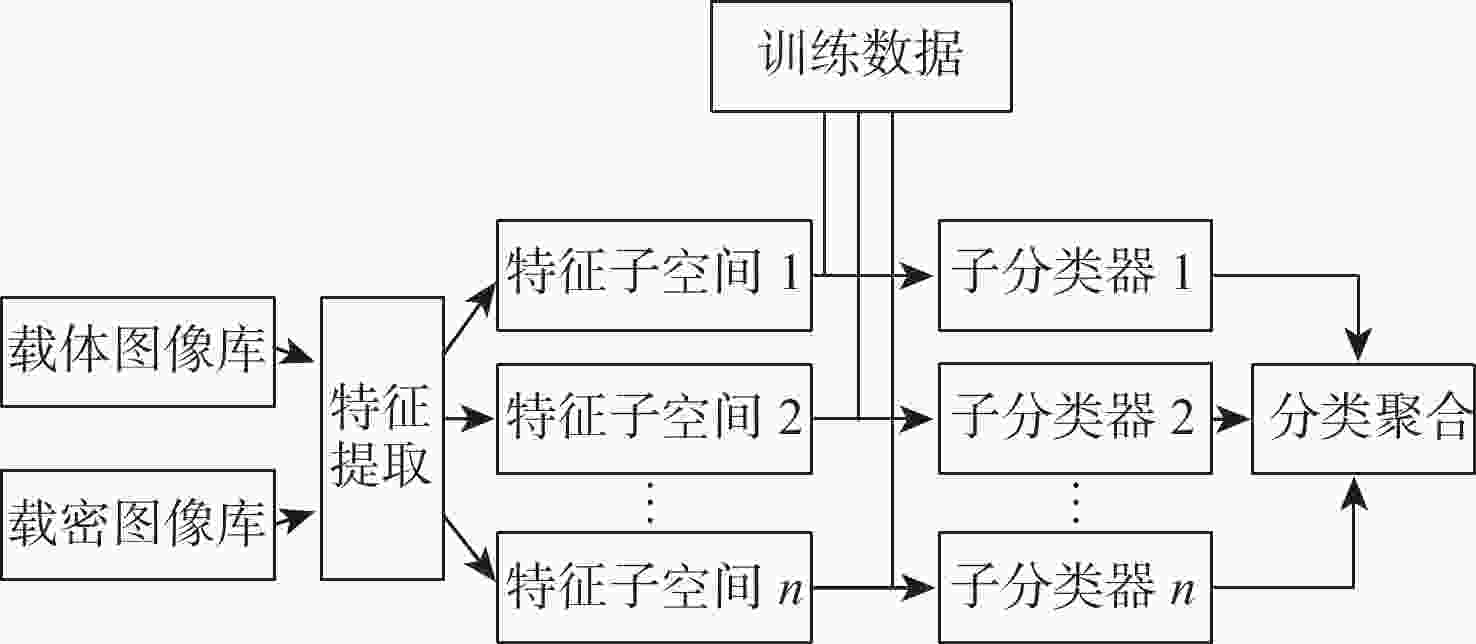
 下载:
下载: