双径向洛伦兹力磁轴承动力学及解耦控制方法

李宗育; 王卫杰; 王丽芬; 任元; 樊亚洪; 李磊

doi:10.13700/j.bh.1001-5965.2023.0262

双径向洛伦兹力磁轴承动力学及解耦控制方法

doi: 10.13700/j.bh.1001-5965.2023.0262

1.
航天工程大学研究生院，北京 101416
2.
航天工程大学宇航科学与技术系，北京 101416
3.
北京控制工程研究所，北京 100190

基金项目:

国家自然科学基金(52075545)

详细信息

通讯作者:
E-mail：wangweijie@126.com

中图分类号: V448.2
计量
- 文章访问数: 123
- HTML全文浏览量: 24
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2023-05-22
- 录用日期: 2023-06-30
- 网络出版日期: 2023-09-01
- 整期出版日期: 2025-05-31

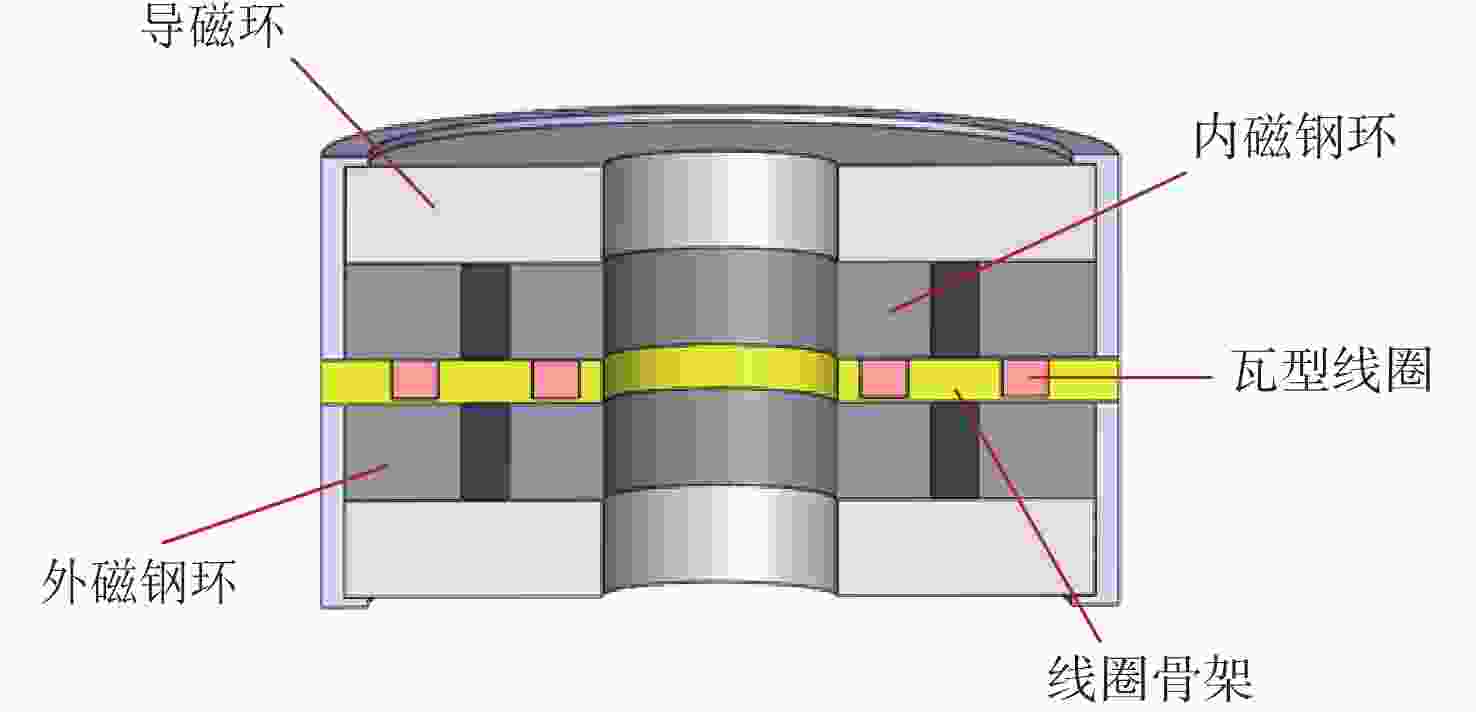
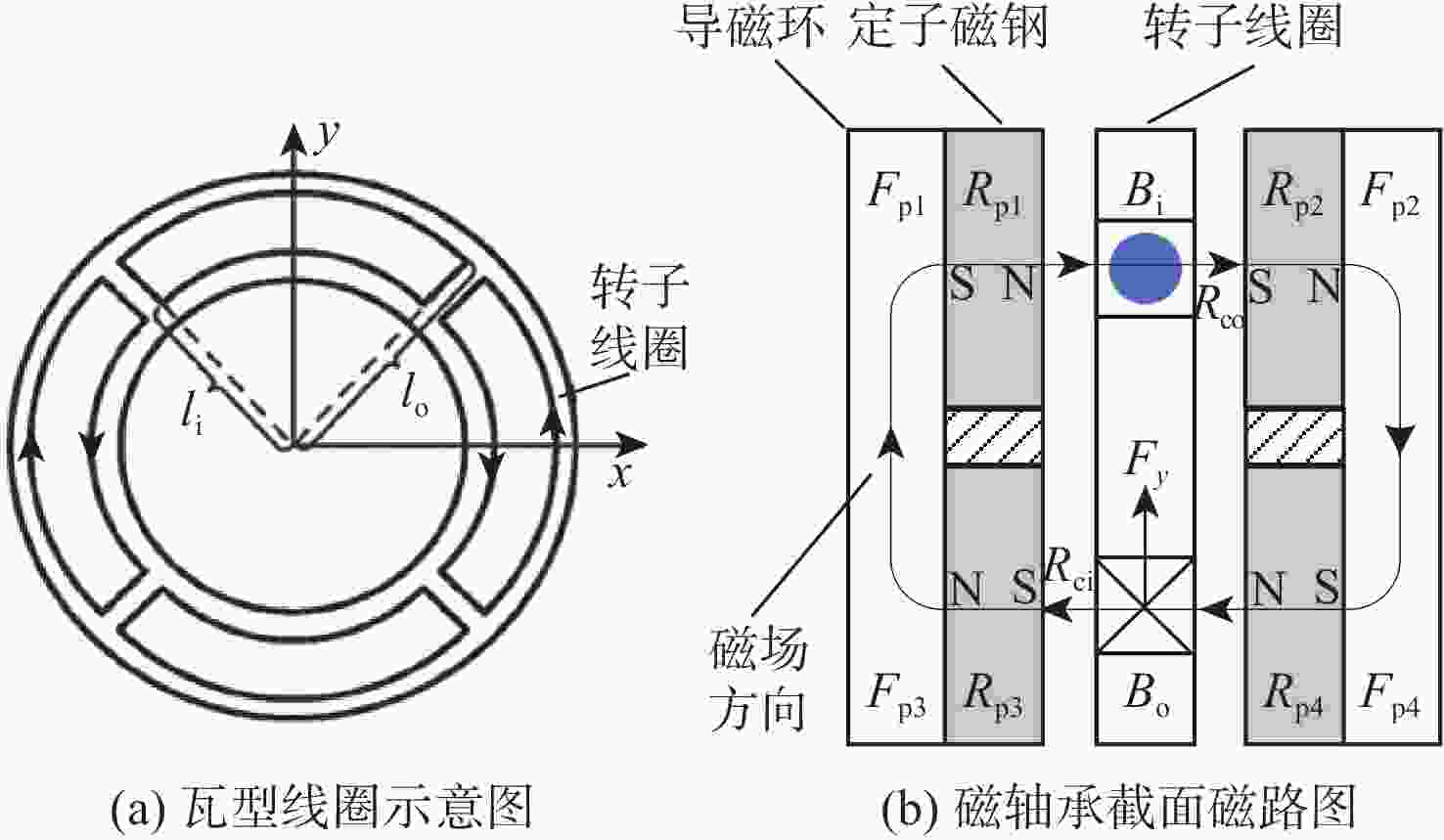
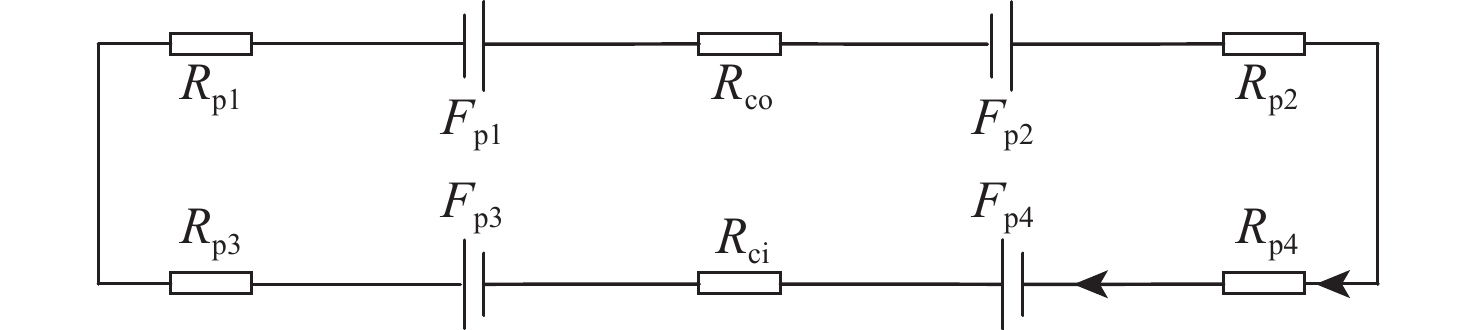
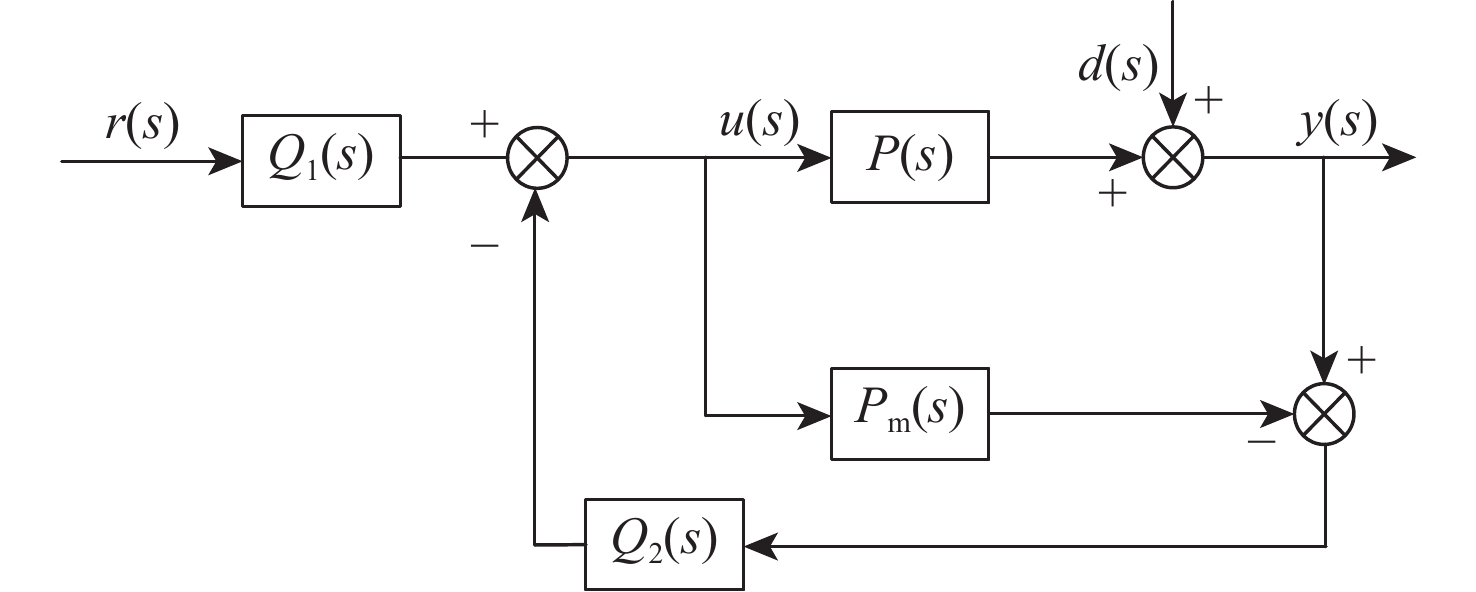
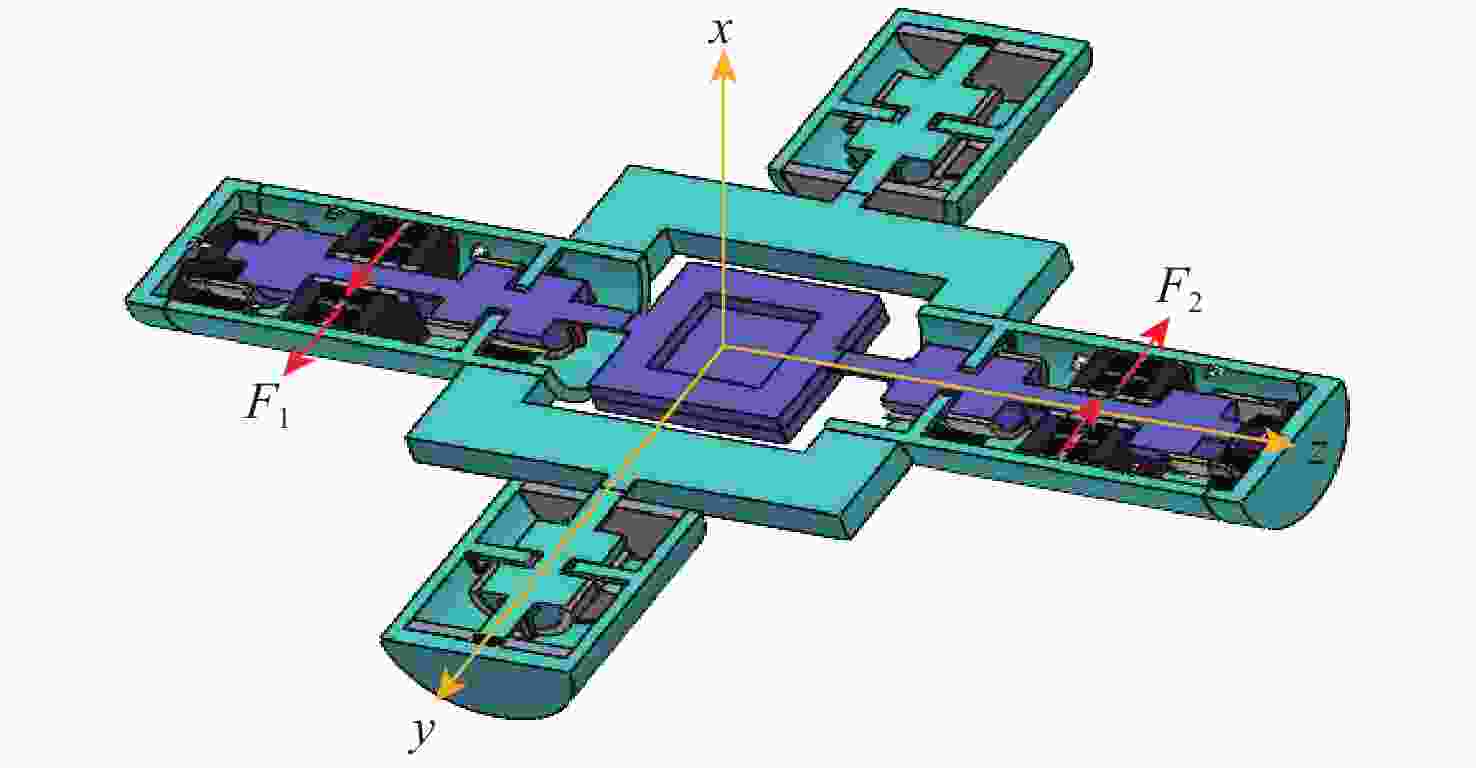
Dynamics and decoupling control method of double radial Lorentz force magnetic bearings

1.
Graduate School，Aerospace Engineering University，Beijing 101416，China
2.
Department of Aerospace Science and Technology，Aerospace Engineering University，Beijing 101416，China
3.
Beijing Institute of Control Engineering，Beijing 100190，China

Funds:

National Natural Science Foundation of China (52075545)

More Information

Corresponding author: E-mail：wangweijie@126.com

摘要

摘要:
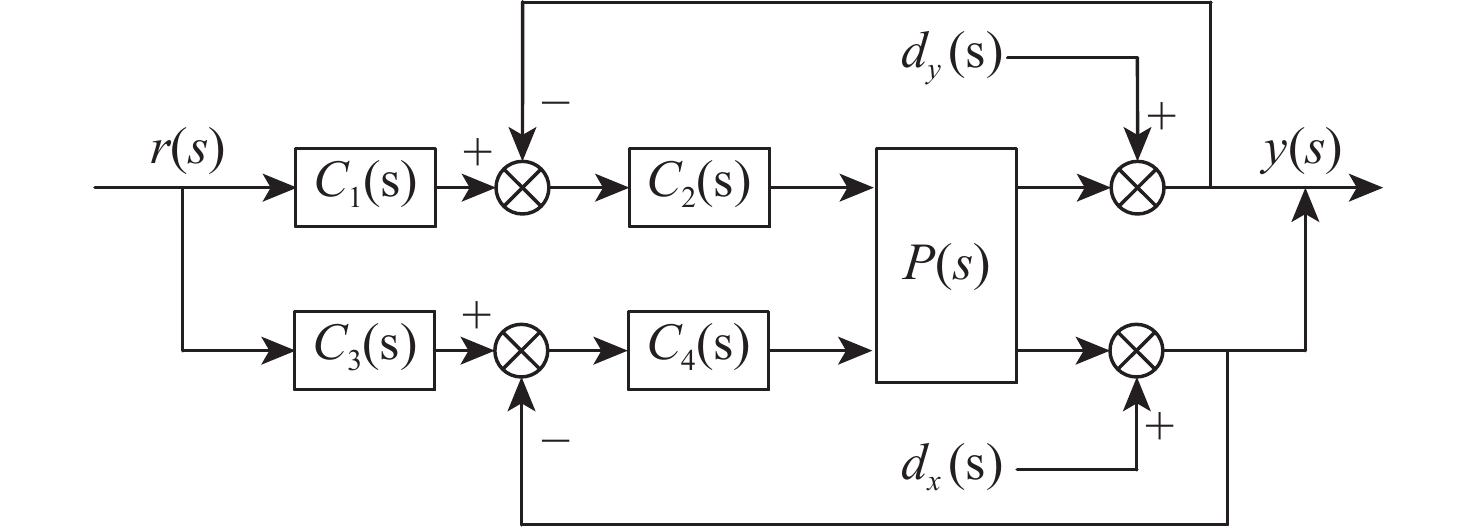
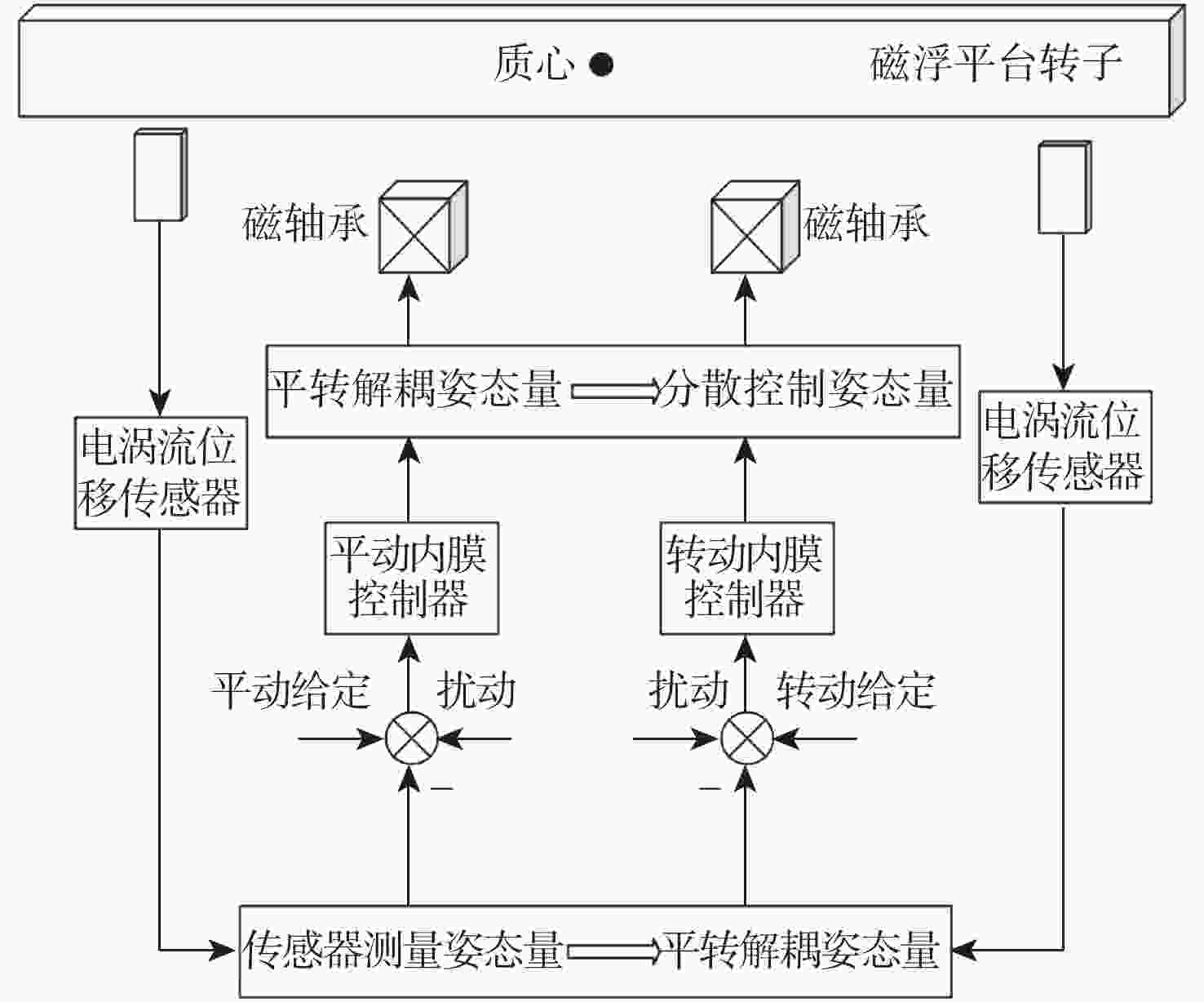
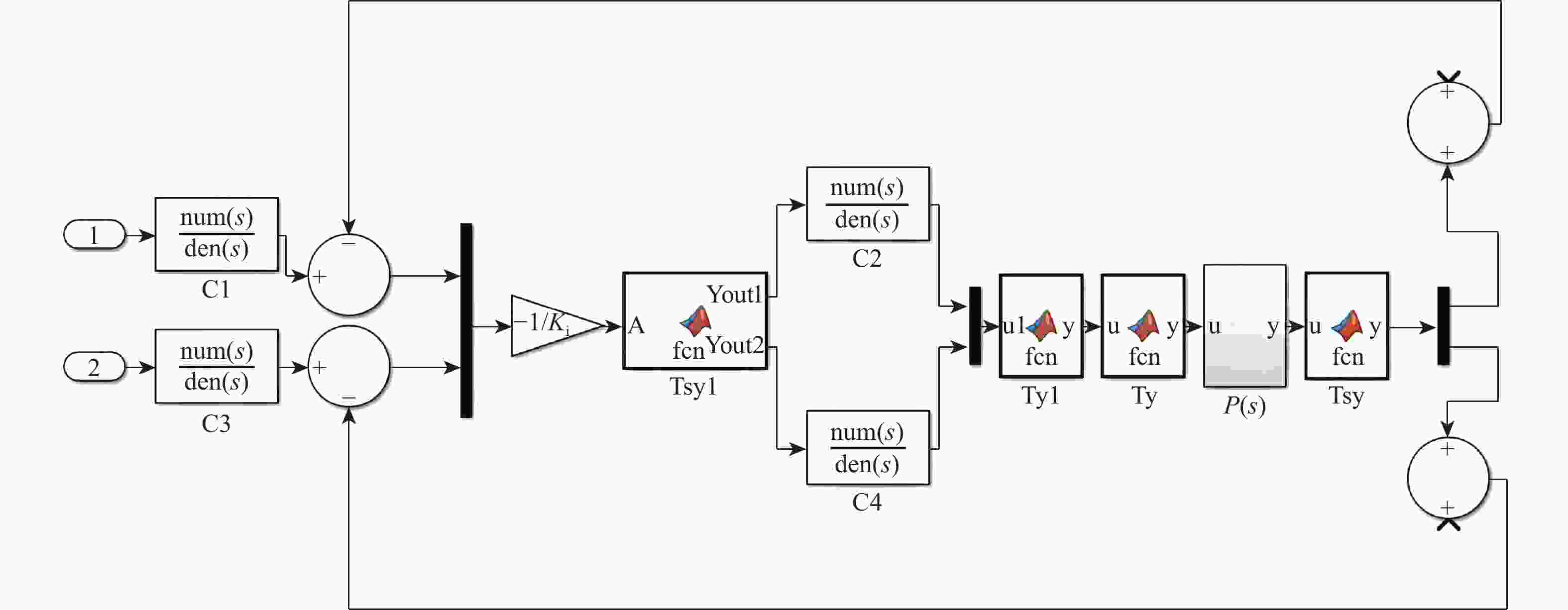
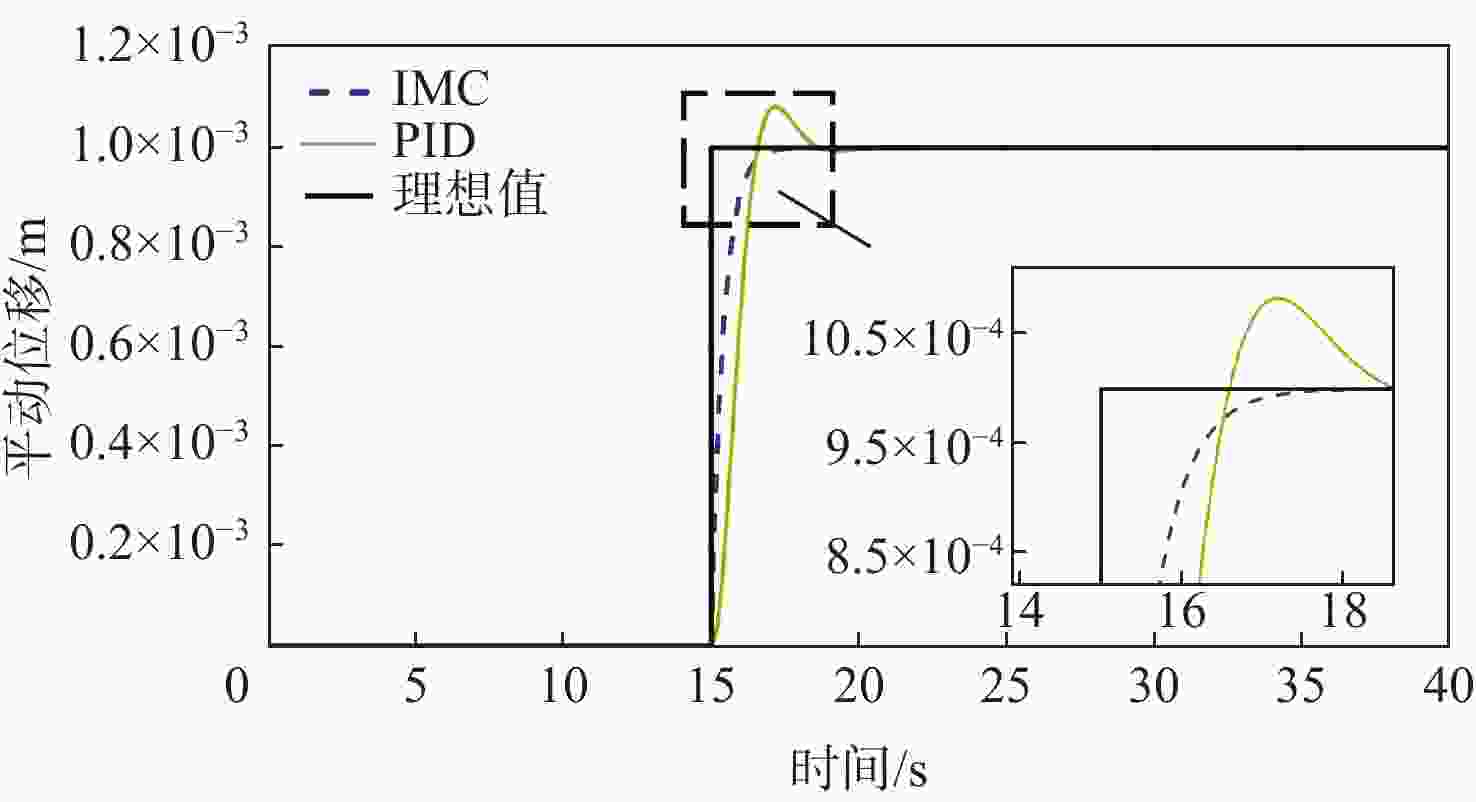
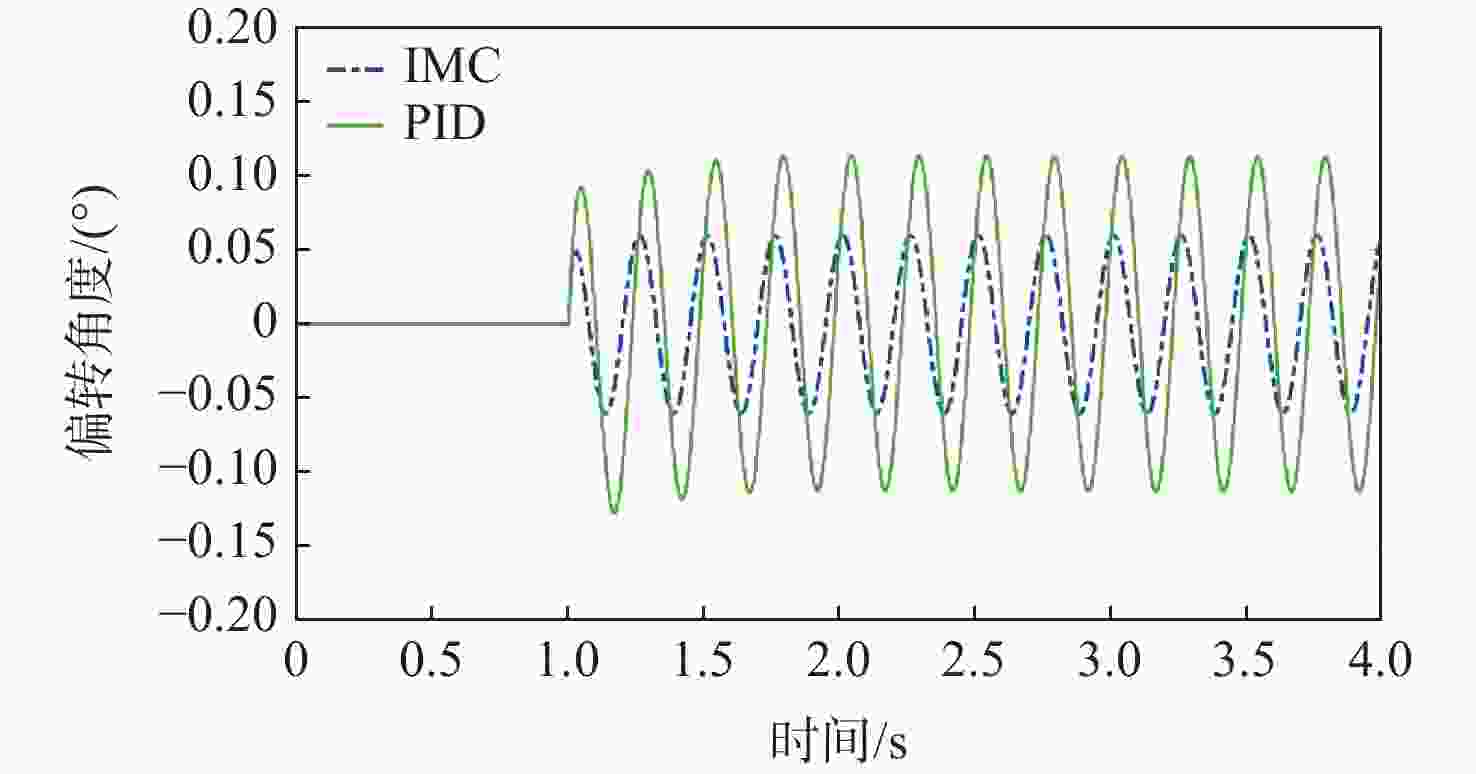
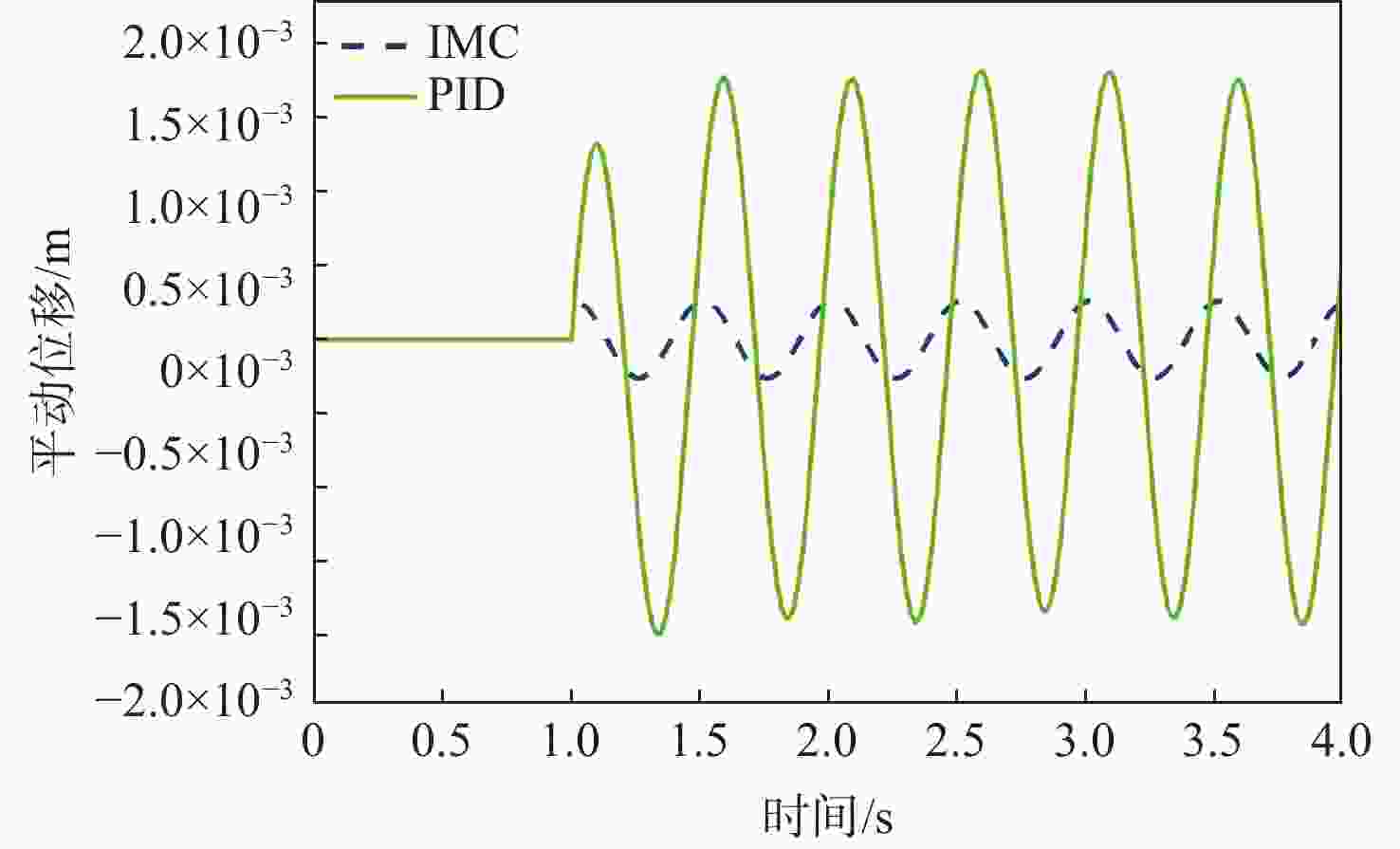
为实现高精度磁浮转台的快速响应和振动抑制，针对洛伦兹力磁悬浮万向稳定平台的高精度解耦控制问题，首先阐明径向洛伦兹力磁轴承(RLFMB)工作原理，基于等效磁路法对单个径向洛伦兹力磁轴承进行动力学建模，构建转子四自由度平转运动动力学模型。设计一种基于内模结构的解耦控制器，通过补灵敏度函数Bode图验证内模控制器强鲁棒的特点。仿真算例结果表明，跟踪性能上，偏转、平动的响应时间分别较PID控制方法降低59.3%和28.2%；抗扰性能上，偏转、平动干扰残余量较PID控制方法降低38.8%和86.2%，此方法可应用于平台对载荷系统的高精、高稳、高动态指向控制。
- 洛伦兹力磁悬浮万向稳定平台 /
- 径向洛伦兹力磁轴承 /
- 解耦控制 /
- 补灵敏度函数 /
- 内模控制
Abstract:
In order to achieve rapid response and vibration suppression of high-precision magnetic levitation turntable and ensure high-precision decoupling control of Lorentz force magnetic levitation omnidirectional stable platform, the working principle of radial Lorentz force magnetic bearings (RLFMBs) was first elucidated. Based on the equivalent magnetic circuit method, a dynamics model of a single RLFMB was established, and a four-degree-of-freedom translational motion dynamics model of the rotor was constructed. A decoupling controller based on the internal model structure was designed, and the strong robustness of the internal model controller was verified by the Bode diagram of the complementary sensitivity function. The simulation results show that in terms of tracking performance, the response time of deflection and translation is reduced by 59.3% and 28.2%, respectively, compared with the proportion-integral-differential (PID) control method. In terms of anti-interference performance, the residual interference of deflection and translation is reduced by 38.8% and 86.2% compared to the PID control method. This method can be applied to high-precision, high-stability, and high dynamic pointing control of the platform’s load system.

HTML全文

图 1 磁轴承主动控制绕X轴旋转示意图

Figure 1. Active control rotation of magnetic bearing around X-axis

下载: 全尺寸图片幻灯片

图 2 单个RLFMB截面结构示意图

Figure 2. Sectional structure of single RLFMB

下载: 全尺寸图片幻灯片

图 3 RLFMB磁路图

Figure 3. Magnetic circuit of RLFMB

下载: 全尺寸图片幻灯片

图 4 等效磁路图

Figure 4. Equivalent magnetic circuit

下载: 全尺寸图片幻灯片

图 5 x通道检测方案

Figure 5. x-channel detection scheme

下载: 全尺寸图片幻灯片

图 6 IMC模型框图

Figure 6. IMC model block diagram

下载: 全尺寸图片幻灯片

图 7 简化IMC模型框图

Figure 7. Simplified IMC model block diagram

下载: 全尺寸图片幻灯片

图 8 平转运动IMC模型框图

Figure 8. Block diagram of IMC model for translation and deflection

下载: 全尺寸图片幻灯片

图 9 洛伦兹力磁浮平台内模控制结构框图

Figure 9. Block diagram of IMC structure of Lorentz force magnetic levitation platform

下载: 全尺寸图片幻灯片

图 10 系统仿真模型

Figure 10. System simulation model

下载: 全尺寸图片幻灯片

图 11 补灵敏度函数Bode图

Figure 11. Bode diagram of complementary sensitivity function

下载: 全尺寸图片幻灯片

图 12 偏转响应曲线对比

Figure 12. Comparison of deflection response curves

下载: 全尺寸图片幻灯片

图 13 平动响应曲线对比

Figure 13. Comparison of translation response curves

下载: 全尺寸图片幻灯片

图 14 偏转干扰曲线对比

Figure 14. Comparison of deflection interference curves

下载: 全尺寸图片幻灯片

图 15 平动干扰曲线对比

Figure 15. Comparison of translation interference curves

下载: 全尺寸图片幻灯片

表 1 洛伦兹力平台系统参数

Table 1. Lorentz force platform system parameters

参数	数值	参数	数值
$ {K_{\text{i}}} $/(N·A⁻¹)	52.5	$ {J}_y/({\text{kg}}\cdot {\mathrm{m}}^{2}) $	1.76
$ {J}_x/({\text{kg}}\cdot {\mathrm{m}}^{2}) $	1.76	$ m{\text{/kg}} $	14.0
$ L{\text{/m}} $	0.15	$ {L_{\text{s}}}{\text{/m}} $	0.20
$ {\lambda _{\text{1}}} $	0.001	$ {\lambda _{\text{2}}} $	0.005
$ {\lambda _{\text{3}}} $	0.05	$ {\lambda _{\text{4}}} $	0.05

下载: 导出CSV

表 2 偏转跟踪实验动态性能指标

Table 2. Dynamic performance index of deflection tracking experiment

控制系统	调节时间/s	响应时间/s	超调量/%
PID	2.56	0.81	12.7
IMC	0.47	0.33	0

下载: 导出CSV

表 3 平动跟踪实验动态性能指标

Table 3. Dynamic performance index of translation tracking experiment

控制系统	调节时间/s	响应时间/s	超调量/%
PID	2.78	1.35	8.3
IMC	1.25	0.97	0

下载: 导出CSV

参考文献(32)

[1]	刘磊. 航天器主动隔振及精确定向控制技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. LIU L. Research on active vibration isolation and precise orientation control technology of spacecraft[D]. Harbin: Harbin Institute of Technology, 2011(in Chinese).
[2]	邓瑞清, 赵岩, 房建成, 等. 磁悬浮飞轮与机械飞轮干扰特性的对比分析[J]. 宇航学报, 2016, 37(8): 917-923. DENG R Q, ZHAO Y, FANG J C, et al. Disturbance characteristics analysis of magnetically suspended and mechanical flywheels[J]. Journal of Astronautics, 2016, 37(8): 917-923(in Chinese).
[3]	崔培玲, 盖玉欢, 房建成, 等. 主被动磁悬浮转子的不平衡振动自适应控制[J]. 光学精密工程, 2015, 23(1): 122-131. doi: 10.3788/OPE.20152301.0122 CUI P L, GAI Y H, FANG J C, et al. Adaptive control for unbalance vibration of active-passive hybrid magnetically suspended rotor[J]. Optics and Precision Engineering, 2015, 23(1): 122-131(in Chinese). doi: 10.3788/OPE.20152301.0122
[4]	张激扬, 刘虎, 王虹, 等. 飞轮扰振特性及振动控制方法[J]. 空间控制技术与应用, 2014, 40(5): 1-7,18. doi: 10.3969/j.issn.1674-1579.2014.05.001 ZHANG J Y, LIU H, WANG H, et al. Microvibration characteristics of flywheels and its vibration control approaches[J]. Aerospace Control and Application, 2014, 40(5): 1-7,18(in Chinese). doi: 10.3969/j.issn.1674-1579.2014.05.001
[5]	RAHMAN Z H, SPANOS J T, LASKIN R A. Multiaxis vibration isolation, suppression, and steering system for space observational applications[C]//Proc. SPIE 3351, Telescope Control Systems III. 1998: 73-81.
[6]	周伟勇. 航天器飞轮动力学建模与振动控制研究[D]. 长沙: 国防科学技术大学, 2012. ZHOU W Y. Research on dynamic modeling and vibration control of spacecraft flywheel[D]. Changsha: National University of Defense Technology, 2012(in Chinese).
[7]	LIU Q, WANG K, REN Y, et al. Novel repeatable launch locking/unlocking device for magnetically suspended momentum flywheel[J]. Mechatronics, 2018, 54: 16-25. doi: 10.1016/j.mechatronics.2018.07.002
[8]	LEE J J, AHN C B, CHOI J, et al. Development of magnetic bearing system for a new third-generation blood pump[J]. Artificial Organs, 2011, 35(11): 1082-1094. doi: 10.1111/j.1525-1594.2011.01376.x
[9]	SAITÔ M, FUKUSHIMA K, SATO N, et al. Development of low disturbance magnetic bearing wheel (MBW) with inclined magnetic poles[J]. The Journal of Space Technology and Science, 2005, 25: 48-68.
[10]	刘彬, 房建成, 刘刚. 一种磁悬浮陀螺飞轮方案设计与关键技术分析[J]. 航空学报, 2011, 32(8): 1478-1487. LIU B, FANG J C, LIU G. Design of a magnetically suspended gyrowheel and analysis of key technologies[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1478-1487(in Chinese).
[11]	李佳益. 磁悬浮微框架动量轮动力学建模与仿真研究[D]. 长沙: 国防科学技术大学, 2012. LI J Y. Research on dynamic modeling and simulation of momentum wheel of magnetic levitation micro-frame[D]. Changsha: National University of Defense Technology, 2012(in Chinese).
[12]	XIANG B, TANG J Q. Suspension and titling of vernier-gimballing magnetically suspended flywheel with conical magnetic bearing and Lorentz magnetic bearing[J]. Mechatronics, 2015, 28: 46-54. doi: 10.1016/j.mechatronics.2015.04.008
[13]	刘强, 赵勇, 曹建树, 等. 新型微框架磁悬浮飞轮用洛伦兹力磁轴承[J]. 宇航学报, 2017, 38(5): 481-489. doi: 10.3873/j.issn.1000-1328.2017.05.006 LIU Q, ZHAO Y, CAO J S, et al. Lorentz magnetic bearing for novel vernier gimballing magnetically suspended flywheel[J]. Journal of Astronautics, 2017, 38(5): 481-489(in Chinese). doi: 10.3873/j.issn.1000-1328.2017.05.006
[14]	赵勇. 新型洛伦兹力磁轴承磁路设计与分析[D]. 北京: 北京石油化工学院, 2019. ZHAO Y. Design and analysis of magnetic circuit of a new Lorentz force magnetic bearing[D]. Beijing: Beijing Institute of Petrochemical Technology, 2019(in Chinese).
[15]	熊颖, 刘强, 李衡, 等. 新型洛伦兹惯性稳定平台控制器设计与实现[J]. 火力与指挥控制, 2022, 47(1): 140-144. doi: 10.3969/j.issn.1002-0640.2022.01.024 XIONG Y, LIU Q, LI H, et al. Design and implementation of a new controller for Lorentz inertial stabilized platform[J]. Fire Control & Command Control, 2022, 47(1): 140-144(in Chinese). doi: 10.3969/j.issn.1002-0640.2022.01.024
[16]	许国锋, 蔡远文, 任元, 等. 洛伦兹力磁轴承磁密均匀度设计与分析[J]. 北京麻豆精品秘国产传媒学报, 2017, 43(3): 559-566. XU G F, CAI Y W, REN Y, et al. Design and analysis on uniformity of magnetic flux density in Lorentz force-type magnetic bearing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43(3): 559-566(in Chinese).
[17]	熊颖. 新型洛伦兹悬浮定位台控制技术研究[D]. 北京: 北京石油化工学院, 2022. XIONG Y. Research on control technology of new Lorenz suspension positioning table[D]. Beijing: Beijing Institute of Petrochemical Technology, 2022(in Chinese).
[18]	GERLACH B, EHINGER M, RAUE H K, et al. Gimballing magnetic bearing reaction wheel with digital controller[C]//The 6th International ESA Conference on Guidance, Navigation and Control Systems[S.l.]:[s.n.]. 2005: 35-40.
[19]	杨磊, 李建普, 杜金龙, 等. 一种径向磁轴承结构及包含该结构的多自由度磁悬浮机构: CN111828475A[P]. 2020-10-27. YANG L, LI J P, DU J L, et al. Radial magnetic bearing and multi-axis levitation system:CN111828475A[P]. 2020-10-27(in Chinese).
[20]	XIANG B, LIU H, YU Y J. Gimbal effect of magnetically suspended flywheel with active deflection of Lorentz-force magnetic bearing[J]. Mechanical Systems and Signal Processing, 2022, 173: 109081. doi: 10.1016/j.ymssp.2022.109081
[21]	张伟, 赵艳彬, 廖鹤, 等. 动静隔离、主从协同控制双超卫星平台设计[J]. 上海航天, 2014, 31(5): 7-11,30. ZHANG W, ZHAO Y B, LIAO H, et al. Design of an active-quiet isolated and master-slave coordination controlled dual-super satellite platform[J]. Aerospace Shanghai, 2014, 31(5): 7-11,30(in Chinese).
[22]	唐忠兴, 姚闯, 何闻, 等. 高精度非接触磁浮机构设计及其输出特性测试研究[J]. 上海航天(中英文), 2020, 37(1): 135-141,149. TANG Z X, YAO C, HE W, et al. Research on high-precision non-contact maglev device design and its output characteristic test[J]. Aerospace Shanghai (Chinese & English), 2020, 37(1): 135-141,149(in Chinese).
[23]	李峥, 赵艳彬, 姚闯, 等. 双超卫星平台柔性线缆构型设计与仿真[J]. 上海航天(中英文), 2022, 39(4): 170-176. LI Z, ZHAO Y B, YAO C, et al. Configuration design and simulation of flexible cables for dual-super satellite platform[J]. Aerospace Shanghai (Chinese & English), 2022, 39(4): 170-176(in Chinese).
[24]	王有懿, 汤亮, 何英姿. 超静平台隔振与指向一体化控制方法[J]. 航天控制, 2016, 34(6): 33-39. WANG Y Y, TANG L, HE Y Z. Integrated control method for vibration isolation and pointing control of ultra quiet platform[J]. Aerospace Control, 2016, 34(6): 33-39(in Chinese).
[25]	赵同爽, 张激扬, 王英广, 等. 磁悬浮旋转关节建模及解耦控制方法研究[J]. 空间控制技术与应用, 2022, 48(2): 71-79. ZHAO T S, ZHANG J Y, WANG Y G, et al. Modeling and decoupling control method of magnetically levitated rotary joints[J]. Aerospace Control and Application, 2022, 48(2): 71-79(in Chinese).
[26]	张井岗, 李临生. 一种二自由度内模控制方法[J]. 工业仪表与自动化装置, 2002(4): 63-65. ZHANG J G, LI L S. A control method performed by a two-degree-of-freedom internal model[J]. Industrial Instrumentation & Automation, 2002(4): 63-65(in Chinese).
[27]	PENG C, FANG J C, XU X B. Mismatched disturbance rejection control for voltage-controlled active magnetic bearing via state-space disturbance observer[J]. IEEE Transactions on Power Electronics, 2015, 30(5): 2753-2762. doi: 10.1109/TPEL.2014.2352366
[28]	KANG M S, LYOU J, LEE J K. Sliding mode control for an active magnetic bearing system subject to base motion[J]. Mechatronics, 2010, 20(1): 171-178. doi: 10.1016/j.mechatronics.2009.09.010
[29]	张玉涵, 蓝益鹏. 磁悬浮平台直线同步电动机TS型模糊控制的研究[J]. 电机与控制应用, 2021, 48(10): 1-6,13. ZHANG Y H, LAN Y P. Research on TS fuzzy control of linear synchronous motor for maglev platform[J]. Electric Machines & Control Application, 2021, 48(10): 1-6,13(in Chinese).
[30]	HOWZE J W, BHATTACHARYYA S P. Robust tracking, error feedback, and two-degree-of-freedom controllers[J]. IEEE Transactions on Automatic Control, 1997, 42(7): 980-983. doi: 10.1109/9.599977
[31]	房建成, 孙津济, 樊亚洪. 磁悬浮惯性动量轮技术[M]. 北京: 国防工业出版社, 2012: 279-280. FANG J C, SUN J J, FAN Y H. Magnetically suspended inertial momentum wheel technology[M]. Beijing: National Defense Industry Press, 2012: 279-280(in Chinese).
[32]	夏长峰, 蔡远文, 任元, 等. 磁悬浮控制敏感陀螺转子前馈解耦内模控制[J]. 北京麻豆精品秘国产传媒学报, 2018, 44(3): 480-488. XIA C F, CAI Y W, REN Y, et al. Feedforward decoupling and internal model control for rotor of magnetically suspended control and sensing gyroscope[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 480-488(in Chinese).