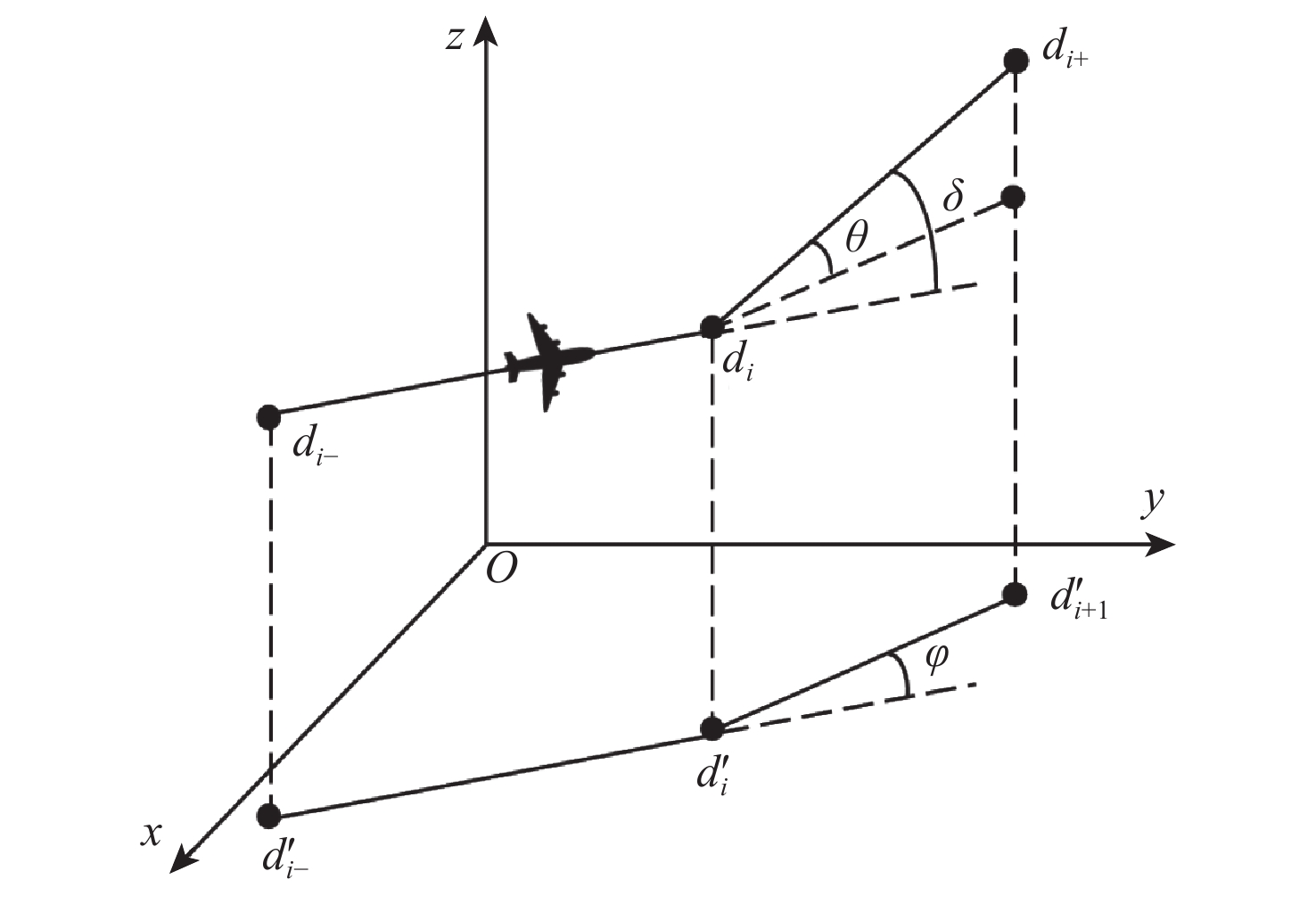
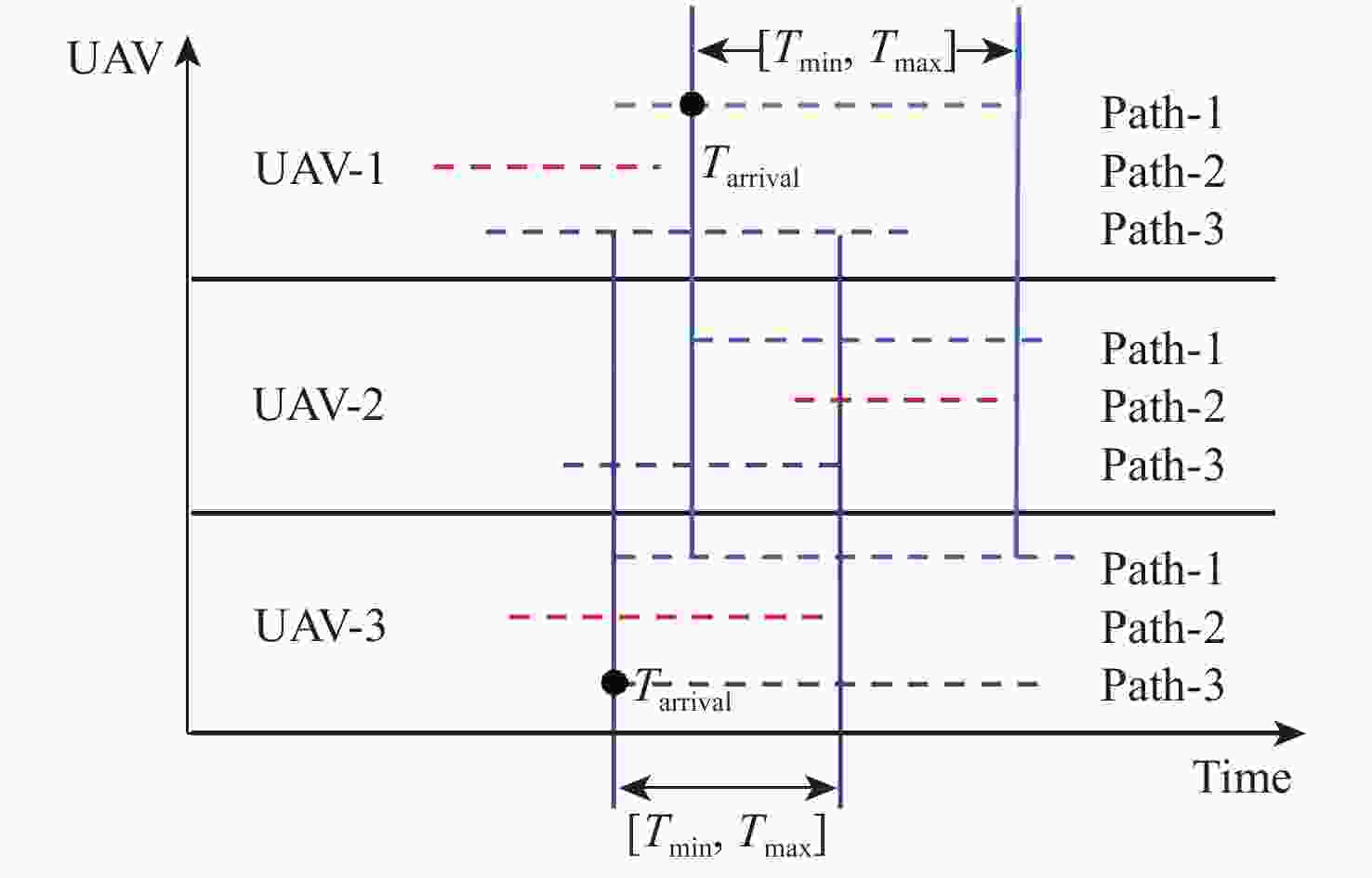
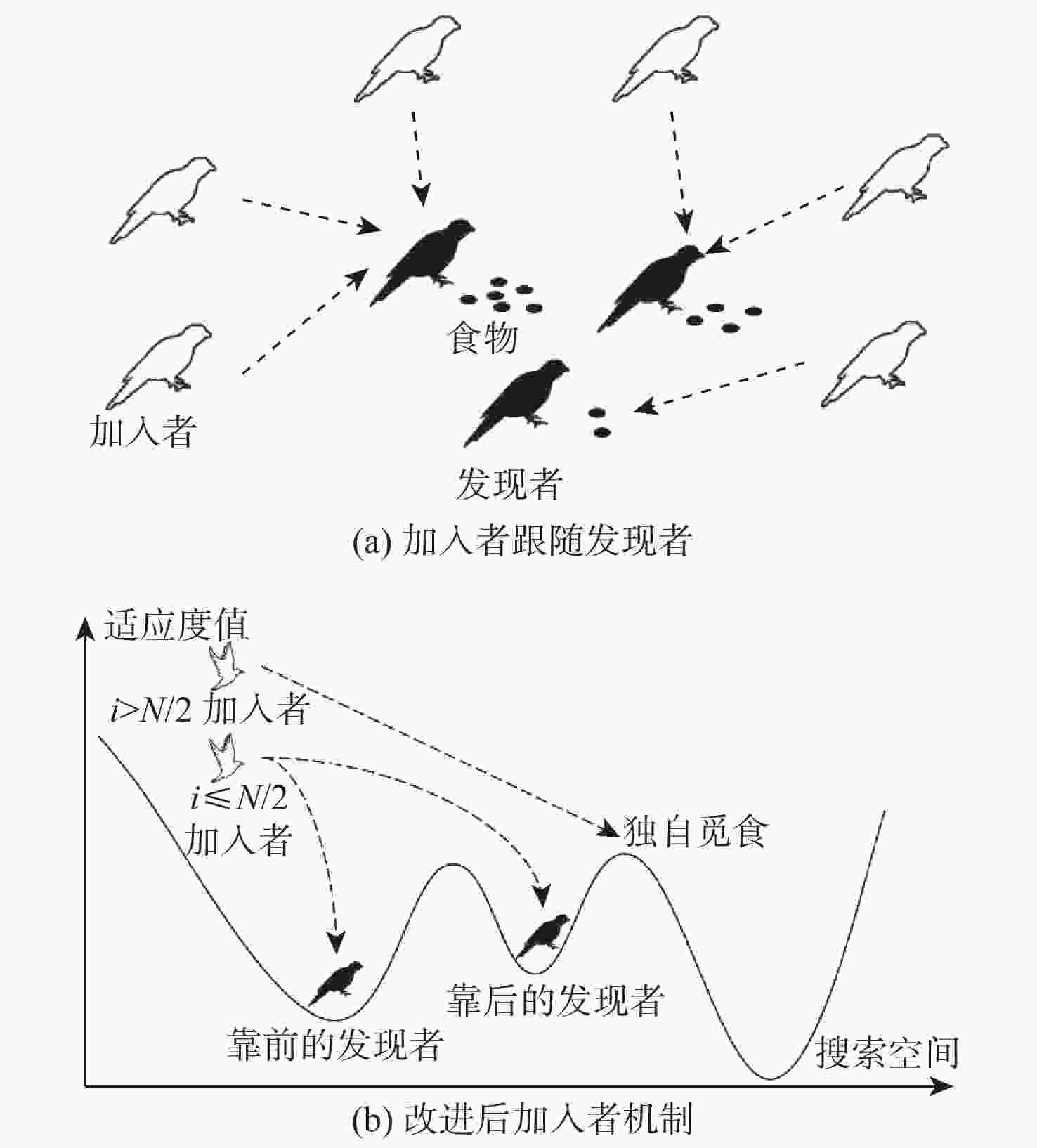
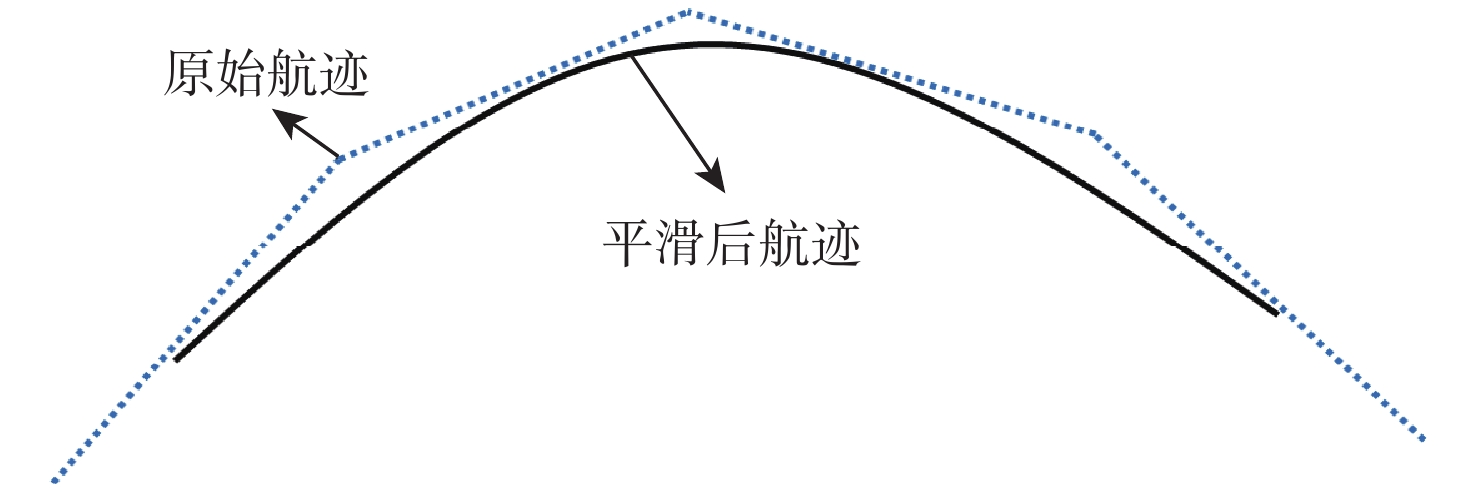
-
摘要:
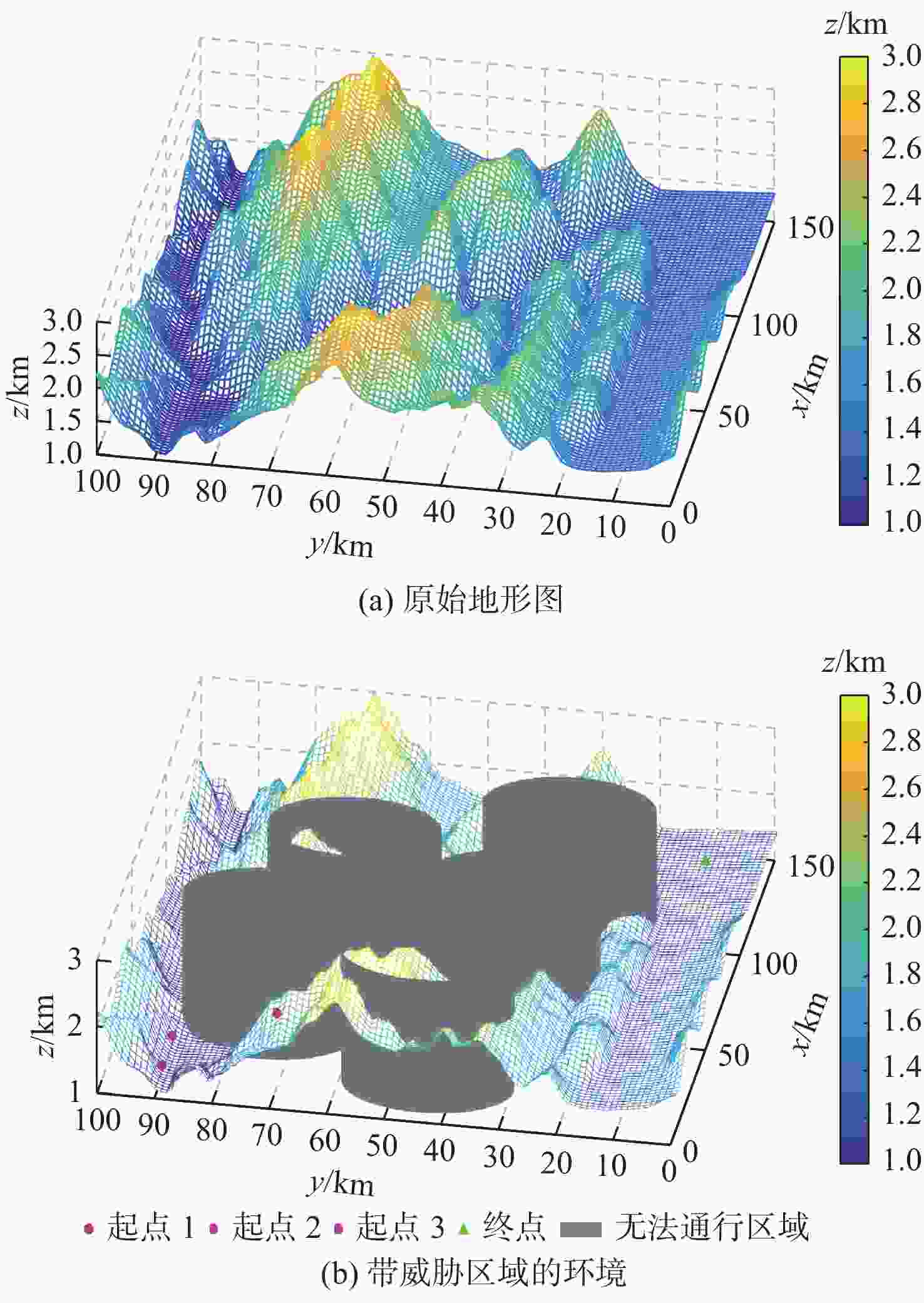
针对多无人机协同航迹规划求解时间要求高、收敛难等问题,提出了一种基于博弈夺食机制和自毁机制的改进麻雀搜索算法(GPSSA)的多无人机协同航迹规划方法。利用分层规划思想分别建立单无人机航迹规划模型和多无人机协同航迹规划模型,将其转化为优化问题。提出博弈夺食机制和自毁机制用以改进麻雀算法,防止其快速丢失种群多样性,增强原算法逃脱局部极值吸引的能力,使得算法搜索方式更加灵活。利用改进麻雀算法对模型进行求解,仿真结果表明,GPSSA算法能够快速完成满足约束的航迹规划,且具有更好的收敛速度、寻优精度和算法鲁棒性。
-
关键词:
- 多无人机协同航迹规划 /
- 麻雀搜索算法 /
- 博弈夺食机制 /
- 自毁机制
Abstract:A multi-UAV cooperative path planning approach based on the self-destruction mechanism and game predatory sparrow search algorithm (GPSSA) is suggested to address the issues of high time requirement and problematic convergence. Firstly, a single UAV path planning model and a multi-UAV cooperative path planning model are established respectively by using the hierarchical planning idea, which is transformed into optimization problems. Then, the game predatory mechanism and self-destruction mechanism is proposed to improve the sparrow algorithm, prevent it from rapidly losing the diversity of the population, enhance the ability of the original algorithm to escape the attraction of local optimum, and make the search mode of the algorithm more flexible. Finally, the improved sparrow algorithm is used to solve the model. The outcomes of the simulation demonstrate how fast and accurately the GPSSA method can plan a path that satisfies the requirements, while also having superior algorithm robustness, convergence speed, and optimization accuracy.
-
表 1 算法参数
Table 1. Algorithm parameters
算法 参数 PSO c1=2 c2=2 Wmix=0.2 Wmax=0.9 DE C=0.2 Fmin=0.2 Fmax=0.8 GWO a=(2→0) SSA S=0.8 P=0.2 GPSSA S=0.8 P=0.2 T=M/20 表 2 单UAV航迹规划仿真结果
Table 2. Simulation results of single UAV track planning
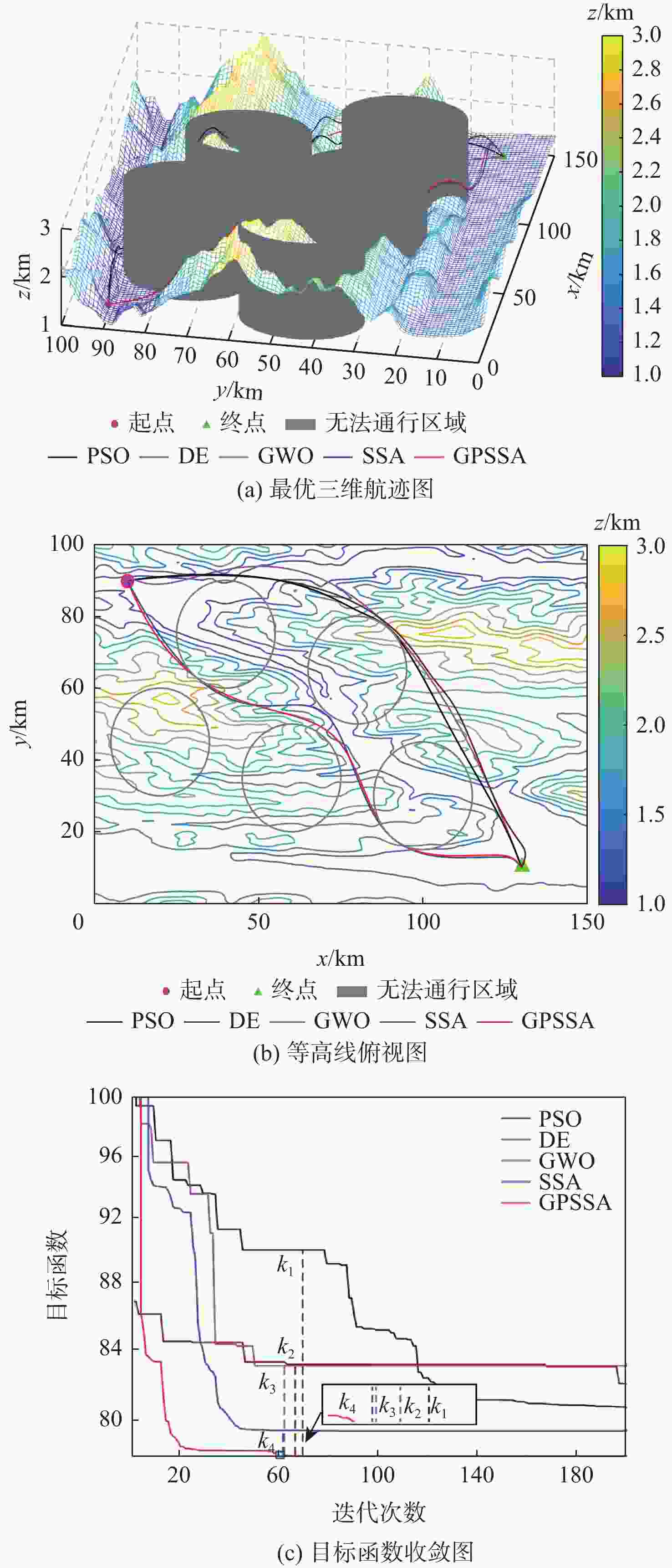
算法 算法平均耗时/s 最优值 最差值 平均值 标准差 PSO 35.635 4 80.824 0 105.188 7 88.608 0 9.129 1 DE 37.275 9 80.620 3 104.277 9 87.412 7 8.164 2 GWO 38.883 7 80.812 4 105.188 7 86.425 2 7.908 0 SSA 39.302 1 79.625 2 107.175 7 92.532 5 9.319 7 GPSSA 40.165 2 76.098 8 89.349 8 82.408 4 3.687 2 表 3 单UAV航迹规划层结果
Table 3. Results of single UAV track planning layer
算法 UAV 最优值 最差值 平均值 标准差 SSA UAV-1 112.675 0 118.649 5 115.701 5 2.439 7 UAV-2 71.428 5 78.462 5 74.902 2 2.872 3 UAV-3 75.642 5 82.067 3 79.826 8 2.961 2 LASSA UAV-1 83.123 9 110.111 0 96.617 5 11.017 0 UAV-2 75.792 2 84.845 5 80.318 9 3.696 0 UAV-3 78.402 9 88.544 8 83.473 9 4.140 4 GPSSA UAV-1 82.193 5 92.160 2 87.557 0 4.104 2 UAV-2 79.716 3 83.056 2 81.801 5 1.484 6 UAV-3 71.292 6 87.313 1 76.845 8 7.406 1 表 4 多UAV协同航迹规划层结果
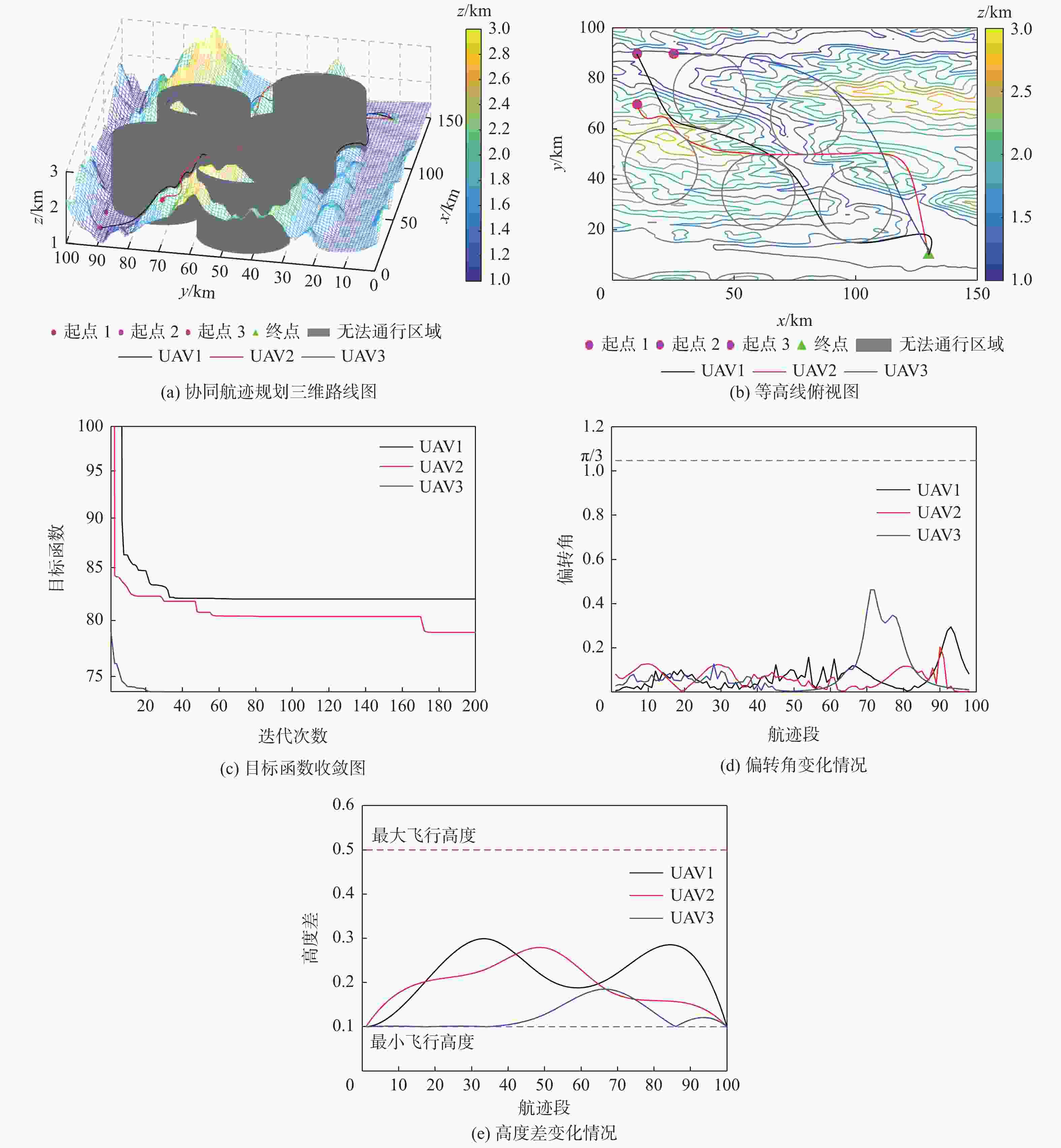
Table 4. Results of multi-UAV cooperative track planning layer
算法 UAV 航迹代价 航迹长度/km 到达时间/s 协同到达时间/s 协同代价 SSA UAV-1 115.78 215.32 [215.32,430.64] [215.32,297.18] 487.98 UAV-2 74.82 148.59 [148.59,297.18] UAV-3 82.07 160.35 [160.35,320.71] LASSA UAV-1 83.12 163.57 [163.57,327.14] [163.57,300.34] 411.03 UAV-2 75.79 150.17 [150.17,300.34] UAV-3 88.54 157.12 [157.12,314.24] GPSSA UAV-1 82.19 163.78 [163.78,327.56] [163.78,284.04] 399.90 UAV-2 82.63 162.86 [162.86,325.73] UAV-3 71.29 142.02 [142.02,284.04] -
[1] 贾高伟, 王建峰. 无人机集群任务规划方法研究综述[J]. 系统工程与电子技术, 2021, 43(1): 99-111. doi: 10.3969/j.issn.1001-506X.2021.01.13JIA G W, WANG J F. Research review of UAV swarm mission planning method[J]. Systems Engineering and Electronics, 2021, 43(1): 99-111(in Chinese). doi: 10.3969/j.issn.1001-506X.2021.01.13 [2] LAVALLE S M, KUFFNER J J. Randomized kinodynamic planning[J]. International Journal of Robotics Research, 2001, 20(5): 378-400. doi: 10.1177/02783640122067453 [3] ZHONG X Y, TIAN J, HU H S, et al. Hybrid path planning based on safe A* algorithm and adaptive window approach for mobile robot in large-scale dynamic environment[J]. Journal of Intelligent & Robotic Systems, 2020, 99(1): 65-77. [4] ALMURIB H A F, NATHAN P T, KUMAR T N. Control and path planning of quadrotor aerial vehicles for search and rescue[C]// SICE Annual Conference. Piscataway: IEEE Press, 2011: 700-705. [5] 王伟, 王华. 基于约束人工势场法的弹载飞行器实时避障航迹规划[J]. 航空动力学报, 2014, 29(7): 1738-1743.WANG W, WANG H. Real-time obstacle avoidance trajectory planning for missile borne air vehicle based on constrained artificial potential field method[J]. Journal of Aerospace Power, 2014, 29(7): 1738-1743(in Chinese). [6] CHEN Y B, LUO G C, MEI Y S, et al. UAV path planning using artificial potential field method updated by optimal control theory[J]. International Journal of Systems Science, 2016, 47(6): 1407-1420. doi: 10.1080/00207721.2014.929191 [7] SUN J Y, TANG J, LAO S Y. Collision avoidance for cooperative UAVs with optimized artificial potential field algorithm[J]. IEEE Access, 2017, 5: 18382-18390. doi: 10.1109/ACCESS.2017.2746752 [8] GALVEZ R L, DADIOS E P, BANDALA A A. Path planning for quadrotor UAV using genetic algorithm[C]// 2014 International Conference on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM). Piscataway: IEEE Press, 2014: 1-6. [9] WANG X F, ZHAO H, HAN T, et al. A grey wolf optimizer using Gaussian estimation of distribution and its application in the multi-UAV multi-target urban tracking problem[J]. Applied Soft Computing, 2019, 78: 240-260. doi: 10.1016/j.asoc.2019.02.037 [10] ZHANG C, ZHEN Z Y, WANG D B, et al. UAV path planning method based on ant colony optimization[C]// 2010 Chinese Control and Decision Conference. Piscataway: IEEE Press, 2010: 3790-3792. [11] PHUNG M D, HA Q P. Safety-enhanced UAV path planning with spherical vector-based particle swarm optimization[J]. Applied Soft Computing, 2021, 107: 107376. doi: 10.1016/j.asoc.2021.107376 [12] PUENTE-CASTRO A, RIVERO D, PAZOS A, et al. A review of artificial intelligence applied to path planning in UAV swarms[J]. Neural Computing and Applications, 2022, 34(1): 153-170. doi: 10.1007/s00521-021-06569-4 [13] BAYERLEIN H, THEILE M, CACCAMO M, et al. Multi-UAV path planning for wireless data harvesting with deep reinforcement learning[J]. IEEE Open Journal of the Communications Society, 2021, 2: 1171-1187. doi: 10.1109/OJCOMS.2021.3081996 [14] NGUYEN K K, DUONG T Q, DO-DUY T, et al. 3D UAV trajectory and data collection optimisation via deep reinforcement learning[J]. IEEE Transactions on Communications, 2022, 70(4): 2358-2371. doi: 10.1109/TCOMM.2022.3148364 [15] SHORAKAEI H, VAHDANI M, IMANI B, et al. Optimal cooperative path planning of unmanned aerial vehicles by a parallel genetic algorithm[J]. Robotica, 2016, 34(4): 823-836. doi: 10.1017/S0263574714001878 [16] PEHLIVANOGLU Y V, PEHLIVANOGLU P. An enhanced genetic algorithm for path planning of autonomous UAV in target coverage problems[J]. Applied Soft Computing, 2021, 112: 107796. doi: 10.1016/j.asoc.2021.107796 [17] SAEED R A, OMRI M, ABDEL-KHALEK S, et al. Optimal path planning for drones based on swarm intelligence algorithm[J]. Neural Computing and Applications, 2022, 34(12): 10133-10155. doi: 10.1007/s00521-022-06998-9 [18] CHOI Y J, RAHIM T, RAMATRYANA I N A, et al. Improved CNN-based path planning for stairs climbing in autonomous UAV with LiDAR sensor[C]// 2021 International Conference on Electronics, Information, and Communication (ICEIC). Piscataway: IEEE Press, 2021: 1-7. [19] ZHANG D F, DUAN H B. Social-class pigeon-inspired optimization and time stamp segmentation for multi-UAV cooperative path planning[J]. Neurocomputing, 2018, 313: 229-246. doi: 10.1016/j.neucom.2018.06.032 [20] 韩统, 汤安迪, 周欢, 等. 基于 LASSA 算法的多无人机协同航迹规划方法[J]. 系统工程与电子技术, 2022, 44(1): 233-241.HAN T, TANG A D, ZHOU H, et al. Multi UAV cooperative path planning method based on Lassa algorithm[J] Systems Engineering and Electronic Technology, 2022, 44 (1): 233-241(in Chinese). [21] JAMSHIDI V, NEKOUKAR V, REFAN M H. Real time UAV path planning by parallel grey wolf optimization with align coefficient on CAN bus[J]. Cluster Computing, 2021, 24(3): 2495-2509. doi: 10.1007/s10586-021-03276-6 [22] HE W J, QI X G, LIU L F. A novel hybrid particle swarm optimization for multi-UAV cooperate path planning[J]. Applied Intelligence, 2021, 51(10): 7350-7364. doi: 10.1007/s10489-020-02082-8 [23] XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34. [24] 闫少强, 杨萍, 朱东林, 等. 基于佳点集的改进麻雀搜索算法[J/OL]. 北京麻豆精品秘 国产传媒学报: 1-13 [2022-03-14]. DOI: 10.13700/j.bh.1001-5965.2021.0730.YAN S Q, YANG P, ZHU D L, et al. Improved sparrow search algorithm based on good point set[J/OL]. Journal of Beijing University of Aeronautics and Astronautics: 1-13 [2022-03-14]. DOI: 10.13700/j.bh.1001-5965.2021.0730(in Chinese). [25] YAN S Q, YANG P, ZHU D L, et al. Improved sparrow search algorithm based on iterative local search[J]. Computational Intelligence and Neuroscience, 2021: 6860503. [26] KENNEDY J, EBERHART R. Particle swarm optimization[C]// Proceedings of ICNN'95 - International Conference on Neural Networks. Piscataway: IEEE Press, 1995: 1942-1948. [27] PRICE K V. Differential evolution[M]// Intelligent Systems Reference Library. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013: 187-214. [28] EMARY E, ZAWBAA H M, HASSANIEN A E. Binary grey wolf optimization approaches for feature selection[J]. Neurocomputing, 2016, 172: 371-381. doi: 10.1016/j.neucom.2015.06.083 -






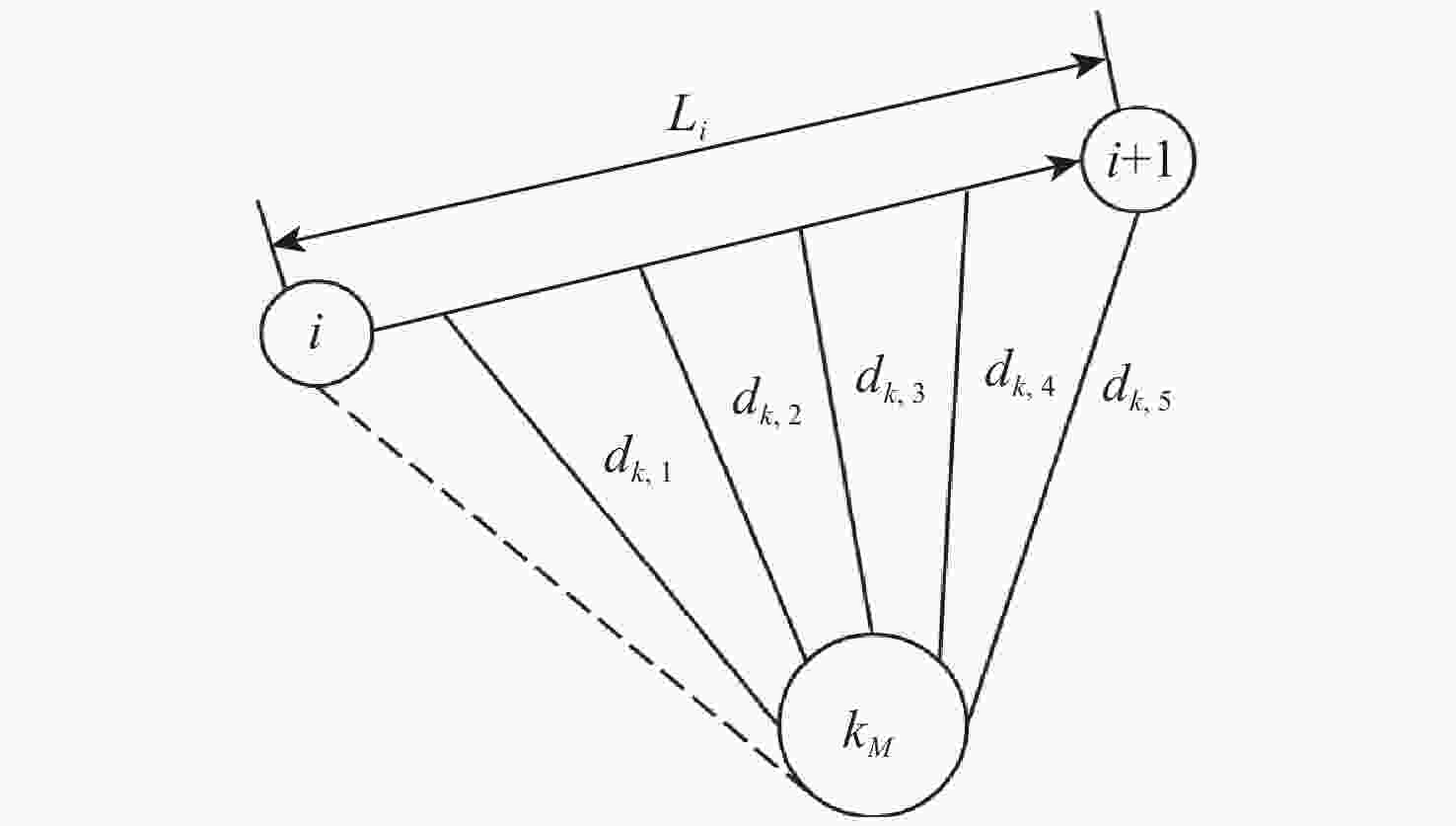
 下载:
下载: