-
摘要:
针对高超声速飞行器再入滑翔段制导问题，提出一种基于粒子群优化-鲸鱼算法的在线制导策略。考虑其约束模型与交班条件，建立了过程约束与终端约束模型。为缩短轨迹生成时间，减少算法计算量，设计了一种能自动满足终端高度、路径角、航程约束的高度-剩余航程飞行剖面。基于阻力系数为常值的前提下，推导了满足航程约束的速度数值解。利用上述模型，设计了一种三参数寻优模型，实现对终端条件的控制。为优化过程约束，提出结合鲸鱼算法和粒子群优化算法的改进鲸鱼算法，克服了粒子群算法易早熟收敛的缺点，提高了求解效率，满足了飞行过程中热流率最小的目标。而后通过将航迹分段的方法，提出一种基于中间点的在线制导方法，对纵向剖面进行在线更新，从而满足终端约束。仿真结果表明，所提方法能高效率的求解最优飞行轨迹。
Abstract:In view of the guidance problem of the hypersonic vehicles in the glide-reentry segment, an online guidance strategy based on improved particle swarm optimization and whale algorithm was proposed. By considering its constraint model and shift conditions, a process constraint and terminal constraint model were established. To shorten the trajectory generation time and reduce the calculation amount of the algorithm, a height-range flight profile that could automatically meet the constraints of terminal height, path angle, and range was designed. Based on the premise that the drag coefficient is a constant value, a numerical solution of velocity that satisfied the range constraint was derived. Based on the above model, a three-parameter optimization model was designed to realize the control of the terminal conditions. To optimize the process constraints, an improved whale algorithm combining the whale algorithm and particle swarm optimization algorithm was proposed to overcome the shortcoming of precocious convergence of the particle swarm optimization algorithm, improve the solution efficiency, and minimize the heat flow rate during the flight. Then, through the method of segmenting the trajectory, an online guidance method based on the mid-point was proposed to update the longitudinal profile online to meet the terminal constraints. The simulation results show that the proposed method can efficiently solve the optimal flight trajectory.
-
图 11 3种智能算法的热流率时间曲线
Figure 11. Heat flow rate-time curves of three intelligent algorithms
表 1 仿真初始条件
Table 1. Initial conditions of simulation
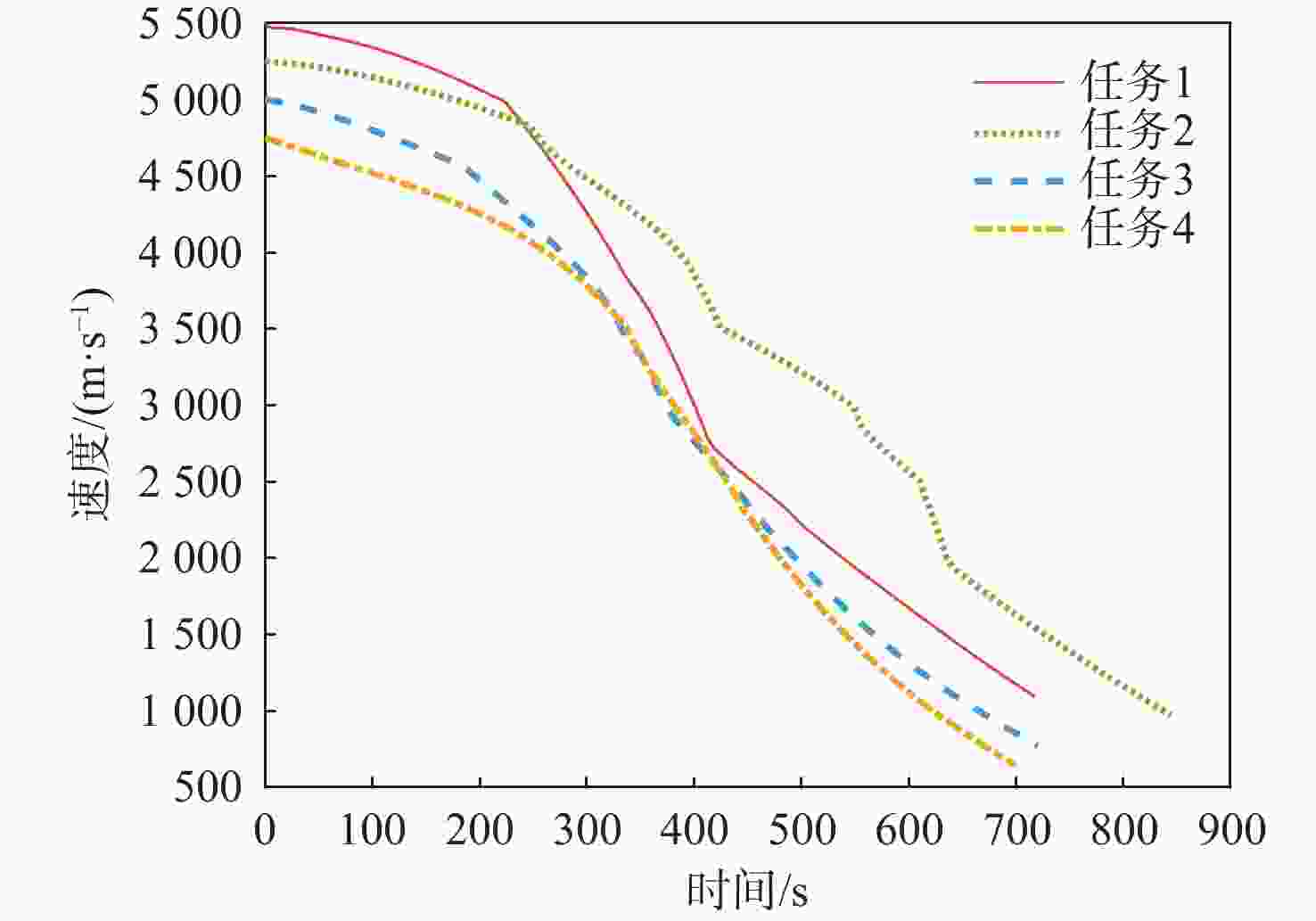
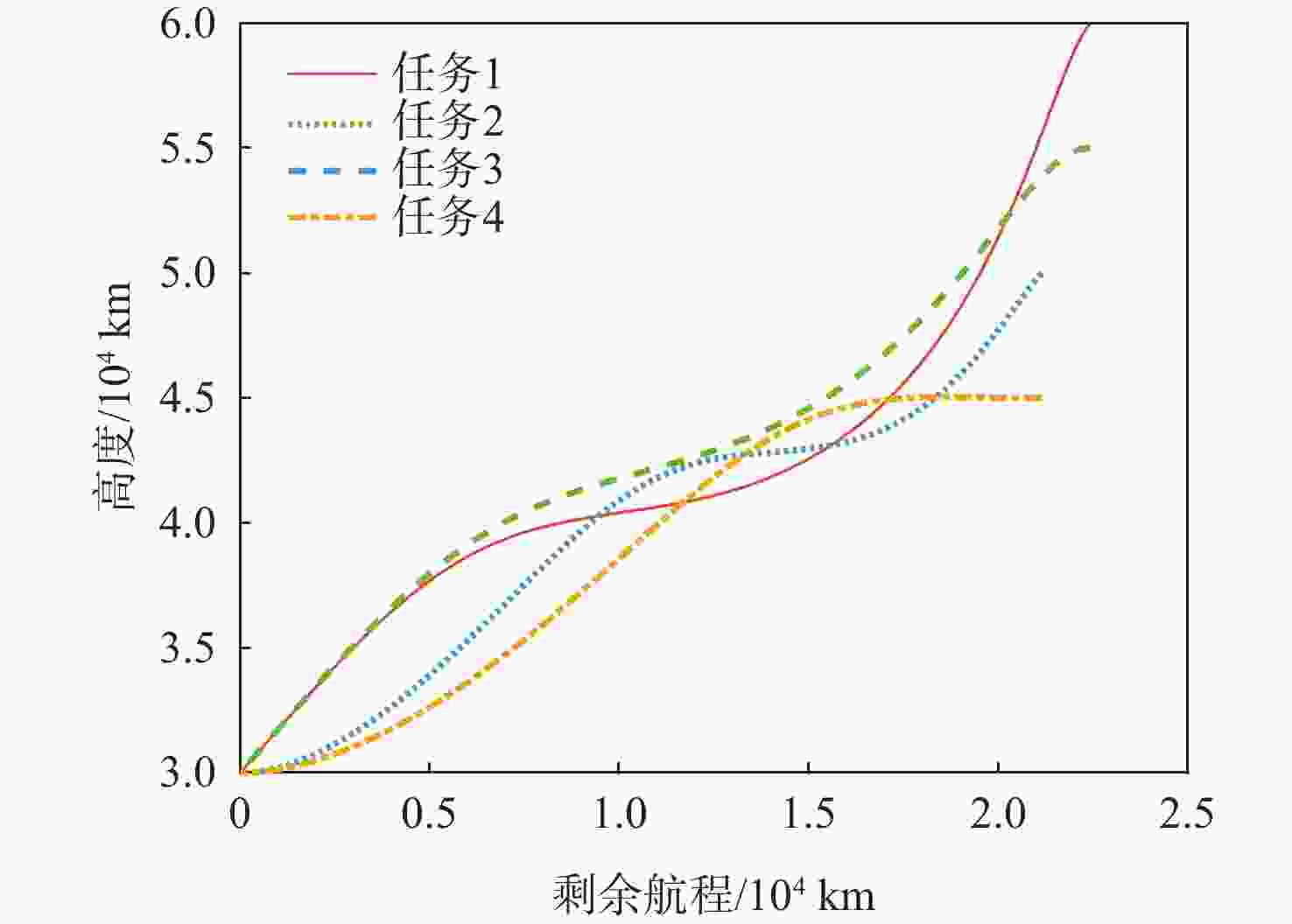
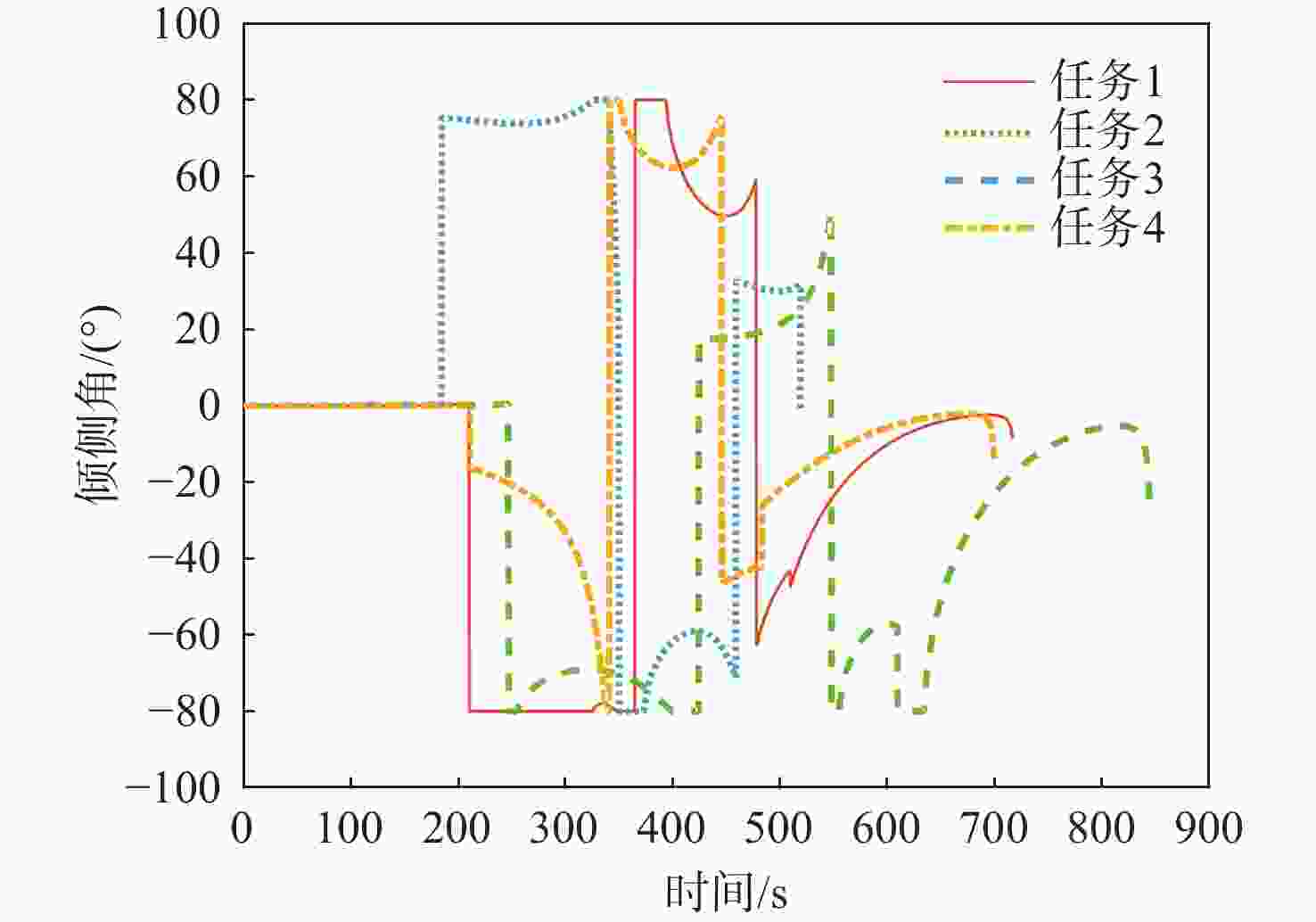
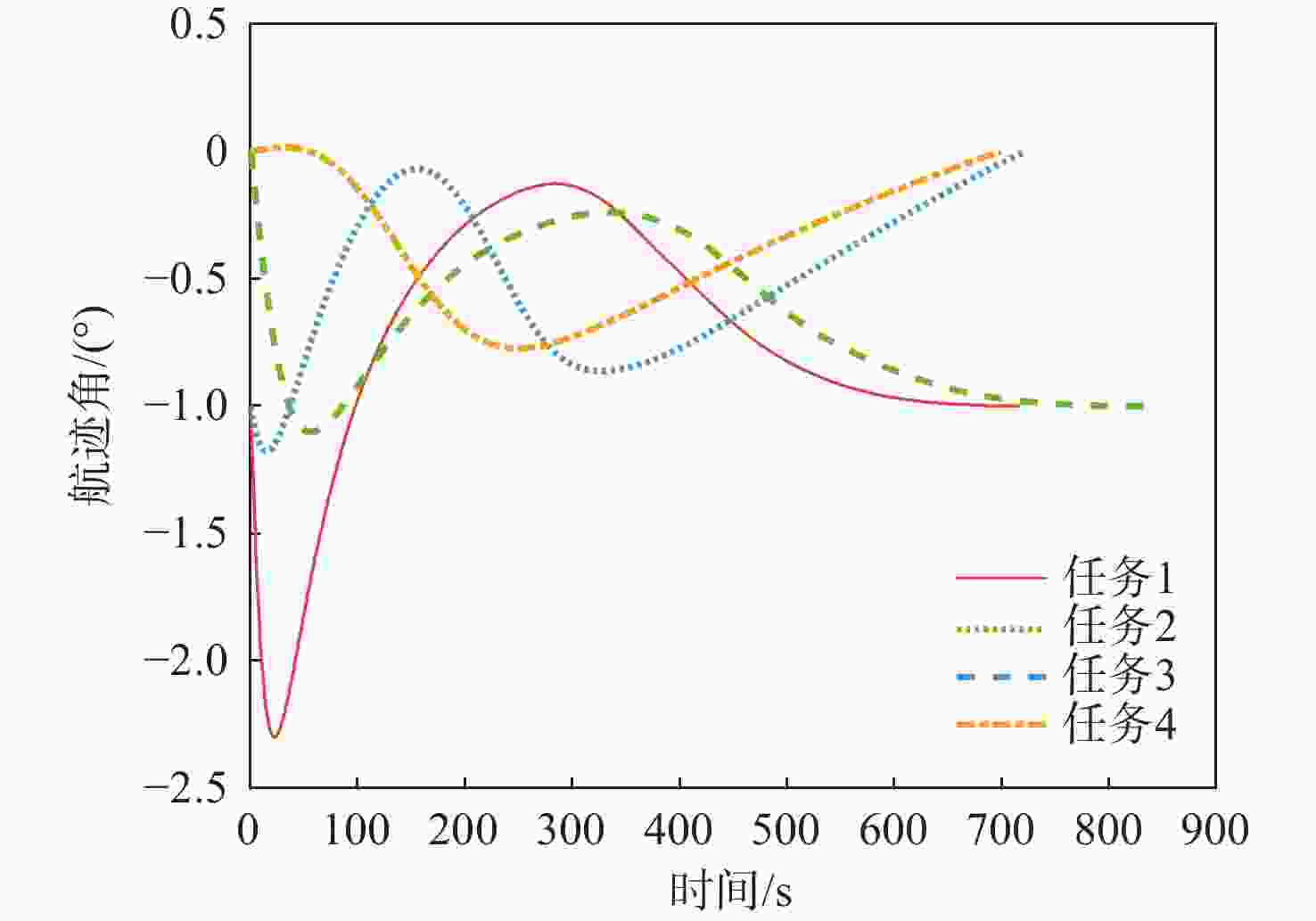
任务 初始位置/(°) 高度/km 速度/(m·s−1) 路径角/(°) 1 (E 90, N 50) 60|30 5500|1100 −1|−1 2 (E 90, N 50) 55|30 5250|950 0|−1 3 (E 90, N 45) 50|30 5000|800 −1|0 4 (E 90, N 45) 45|30 4750|650 0|0 
下载: 导出CSV
表 2 仿真结果
Table 2. Simulation result
任务 $ \left| {\Delta V} \right|/({\text{m}} \cdot {\text{s}}^{-1}) $ $\left| {\Delta \gamma } \right|$/(°) $\left| {\Delta h} \right|/{\text{km}}$ $ \left| {\Delta {R_{\mathrm{L}}}} \right| / {\text{km}} $ 1 4.17 3.62×10−5 4.70×10−2 2.69 2 21.92 2.07×10−6 3.40×10−2 1.94 3 29.64 6.58×10−5 1.11×10−2 1.39 4 17.20 2.64×10−5 1.83×10−3 0.89
下载: 导出CSV
表 3 终端约束相对误差
Table 3. Relative error of terminal constraint
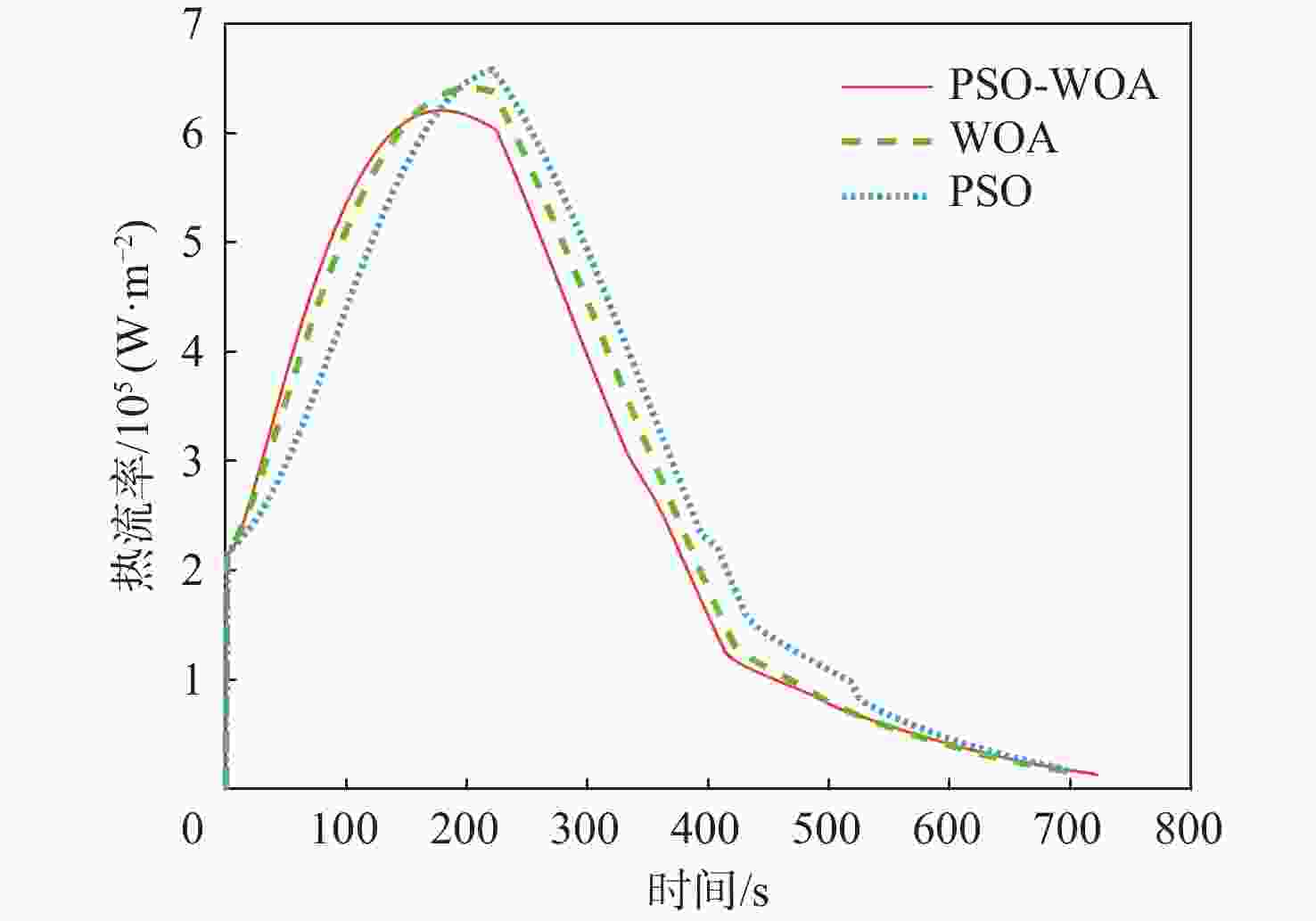
任务 相对误差/% $\Delta V$ $\Delta \gamma $ $\Delta h $ $\Delta {R_{\mathrm{L}}} $ 1 0.38 0.0036 0.16 0.120 2 2.31 0.00021 0.11 0.086 3 3.71 0.0066 0.037 0.066 4 2.64 0.0026 0.0061 0.042
下载: 导出CSV
表 4 3种智能算法的仿真结果
Table 4. Simulation results of three intelligent algorithms
算法 $ \left| {\Delta V} \right| / ({\text{m}} \cdot {\text{s}}^{-1}) $ $\left| {\Delta \gamma } \right| $/(°) $\left| {\Delta h} \right| /{\text{km}} $ $ \left| {\Delta {R_{\mathrm{L}}}} \right| /{\text{km}} $ PSO-WOA 16.28 1.48×10−6 1.21×10−3 0.56 WOA 35.43 1.66×10−6 2.36×10−2 0.98 PSO 11.41 1.17×10−5 2.15×10−2 1.23
下载: 导出CSV
-
[1] 李帆, 张云飞, 李航宇, 等. 2021年世界防空反导综述及对我国发展的启示[J]. 战术导弹技术, 2022(3): 34-39.LI F, ZHANG Y F, LI H Y, et al. Review of world air and missile defense in 2021 and the enlightenment to China’s development[J]. Tactical Missile Technology, 2022(3): 34-39(in Chinese). [2] 张灿, 王轶鹏, 叶蕾. 国外近十年高超声速飞行器技术发展综述[J]. 战术导弹技术, 2020(6): 81-86.ZHANG C, WANG Y P, YE L. Summary of the technological development of overseas hypersonics in the past ten years[J]. Tactical Missile Technology, 2020(6): 81-86(in Chinese). [3] 陈冰, 郑勇, 章后甜, 等. 临近空间高超声速飞行器导航技术发展综述[J]. 飞航导弹, 2021(12): 57-62.CHEN B, ZHENG Y, ZHANG H T, et al. Overview of the development of navigation technology for hypersonic vehicles in near space[J]. Aerodynamic Missile Journal, 2021(12): 57-62(in Chinese). [4] 吴了泥. 可重复使用运载器亚轨道再入段制导与控制技术研究[D]. 南京: 南京麻豆精品秘 国产传媒, 2009.WU L N. Research on guidance and control technology of sub-orbital reentry phase of reusable launch vehicle[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009(in Chinese). [5] ELNAGAR G N, KAZEMI M A. Pseudospectral Chebyshev optimal control of constrained nonlinear dynamical systems[J]. Computational Optimization and Applications, 1998, 11(2): 195-217. doi: 10.1023/A:1018694111831 [6] 呼卫军, 周军, 常晶, 等. RLV应急再入轨迹规划问题的动态伪谱法求解[J]. 宇航学报, 2015, 36(11): 1255-1261.HU W J, ZHOU J, CHANG J, et al. Emergency reentry trajectory planning for reusable launch vehicle based on dynamic Gauss pseudo-spectral[J]. Journal of Astronautics, 2015, 36(11): 1255-1261(in Chinese). [7] WANG T, ZHANG H B, ZENG L, et al. A robust predictor-corrector entry guidance[J]. Aerospace Science and Technology, 2017, 66: 103-111. doi: 10.1016/j.ast.2017.03.010 [8] 刘欣, 李建林, 葛健全, 等. 滑翔式飞行器再入弹道设计[J]. 弹箭与制导学报, 2011, 31(6): 161-164.LIU X, LI J L, GE J Q, et al. Reentry trajectory design for glide-reentry vehicle[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(6): 161-164(in Chinese). [9] 伍元培, 王阳, 赵爱红, 等. 基于深度学习网络的高超声速飞行器避障轨迹规划方法[J]. 战术导弹技术, 2022(1): 53-59.WU Y P, WANG Y, ZHAO A H, et al. Obstacle avoidance trajectory planning of hypersonic vehicle based on deep learning network[J]. Tactical Missile Technology, 2022(1): 53-59(in Chinese). [10] 冯林爽, 刘磊, 王永骥. 基于PSO和SQP混合优化算法的高超声速飞行器轨迹优化[C]//第27届中国控制与决策会议论文集. 北京: 北京麻豆精品秘 国产传媒出版社, 2015: 1527-1531.FENG L S, LIU L, WANG Y J. Hypersonic vehicle trajectory optimization based on PSO and SQP hybrid optimization algorithm [C]//Proceedings of the 27th China Control and Decision Making Conference. Beijing: Beihang University Press, 2015: 1527-1531(in Chinese). [11] 高岳林, 杨钦文, 王晓峰, 等. 新型群体智能优化算法综述[J]. 郑州大学学报(工学版), 2022(3): 21-30.GAO Y L, YANG Q W, WANG X F, et al. Overview of new swarm intelligence optimization algorithms[J]. Journal of Zhengzhou University (Engineering Edition), 2022(3): 21-30(in Chinese). [12] 黄清宝, 李俊兴, 宋春宁, 等. 基于余弦控制因子和多项式变异的鲸鱼优化算法[J]. 控制与决策, 2020, 35(3): 559-568.HUANG Q B, LI J X, SONG C N, et al. Whale optimization algorithm based on cosine control factor and polynomial mutation[J]. Control and Decision, 2020, 35(3): 559-568(in Chinese). [13] SAAFAN M M, EL-GENDY E M. IWOSSA: An improved whale optimization salp swarm algorithm for solving optimization problems[J]. Expert Systems with Applications, 2021, 176: 114901. doi: 10.1016/j.eswa.2021.114901 [14] ABD ELAZIZ M, LU S F, HE S B. A multi-leader whale optimization algorithm for global optimization and image segmentation[J]. Expert Systems with Applications, 2021, 175: 114841. doi: 10.1016/j.eswa.2021.114841 [15] AGRAWAL R K, KAUR B, SHARMA S. Quantum based whale optimization algorithm for wrapper feature selection[J]. Applied Soft Computing, 2020, 89: 106092. doi: 10.1016/j.asoc.2020.106092 [16] ZHOU H Y, WANG X G, CUI N G. A novel reentry trajectory generation method using improved particle swarm optimization[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3212-3223. doi: 10.1109/TVT.2019.2899917 [17] LI Z H, HU C, DING C B, et al. Stochastic gradient particle swarm optimization based entry trajectory rapid planning for hypersonic glide vehicles[J]. Aerospace Science and Technology, 2018, 76: 176-186. doi: 10.1016/j.ast.2018.01.033 [18] 徐慧, 蔡光斌, 穆朝絮, 等. 高超声速滑翔飞行器全程总红外辐射最小的轨迹优化(特邀)[J]. 红外与激光工程, 2022, 51(4): 3788.XU H, CAI G B, MU Z X, et al. Trajectory optimization of hypersonic glide vehicle with minimum total infrared radiation (Invited)[J]. Infrared and Laser Engineering, 2022, 51(4): 3788(in Chinese). [19] 周宏宇, 王小刚, 赵亚丽, 等. 空天飞行器返回滑翔段在线制导方法[J]. 宇航学报, 2021, 42(2): 175-184.ZHOU H Y, WANG X G, ZHAO Y L, et al. Online guidance for aerospace vehicle in return-gliding phase[J]. Journal of Astronautics, 2021, 42(2): 175-184(in Chinese). [20] ZHANG W Q, CHEN W C, YU W B. Entry guidance for high-L/D hypersonic vehicle based on drag-vs-energy profile[J]. ISA Transactions, 2018, 83: 176-188. doi: 10.1016/j.isatra.2018.08.012 [21] 周宏宇. 组合动力可重复使用运载器三维轨迹优化与在线制导方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.ZHOU H Y. Research on 3D trajectory optimization and online guidance method of combined power reusable launch vehicle[D]. Harbin: Harbin Institute of Technology, 2019(in Chinese). [22] HAMEED A S, BINDU G R. Single segment approach and landing guidance and control for an unpowered reusable launch vehicle[J]. Aerospace Science and Technology, 2021, 115: 106777. doi: 10.1016/j.ast.2021.106777 [23] 徐慧, 蔡光斌, 张胜修. 高超声速滑翔飞行器再入气动系数改进拟合模型[J]. 宇航学报, 2021, 42(9): 1139-1149.XU H, CAI G B, ZHANG S X. Modified aerodynamic coefficient fitting models of hypersonic gliding vehicle in reentry phase[J]. Journal of Astronautics, 2021, 42(9): 1139-1149(in Chinese). [24] MIRJALILI S, LEWIS A. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67. doi: 10.1016/j.advengsoft.2016.01.008 -
下载:
点击查看大图
计量
- 文章访问数: 491
- HTML全文浏览量: 305
- PDF下载量: 66
- 被引次数: 0
