多策略融合的改进黑猩猩优化算法

张福兴; 高腾; 吴泓达

doi:10.13700/j.bh.1001-5965.2022.0891

多策略融合的改进黑猩猩优化算法

doi: 10.13700/j.bh.1001-5965.2022.0891

大连工业大学机械工程与自动化学院，大连 116034

基金项目:

辽宁省教育厅高校基本科研项目(JYTZD2023023)

详细信息

通讯作者:
E-mail：gaoteng@dlpu.edu.cn

中图分类号: TM561.2
计量
- 文章访问数: 318
- HTML全文浏览量: 108
- PDF下载量: 21
- 被引次数: 0
出版历程
- 收稿日期: 2022-11-04
- 录用日期: 2022-12-30
- 网络出版日期: 2024-07-17
- 整期出版日期: 2025-01-31

Improved chimpanzee search algorithm based on multi-strategy fusion and its application

School of Mechanical Engineering and Automation，Dalian Polytechnic University，Dalian 116034，China

Funds:

Basic Scientific Research Project of Higher Education Institutions in Liaoning Province (JYTZD2023023)

More Information

Corresponding author: E-mail：gaoteng@dlpu.edu.cn

摘要

摘要:
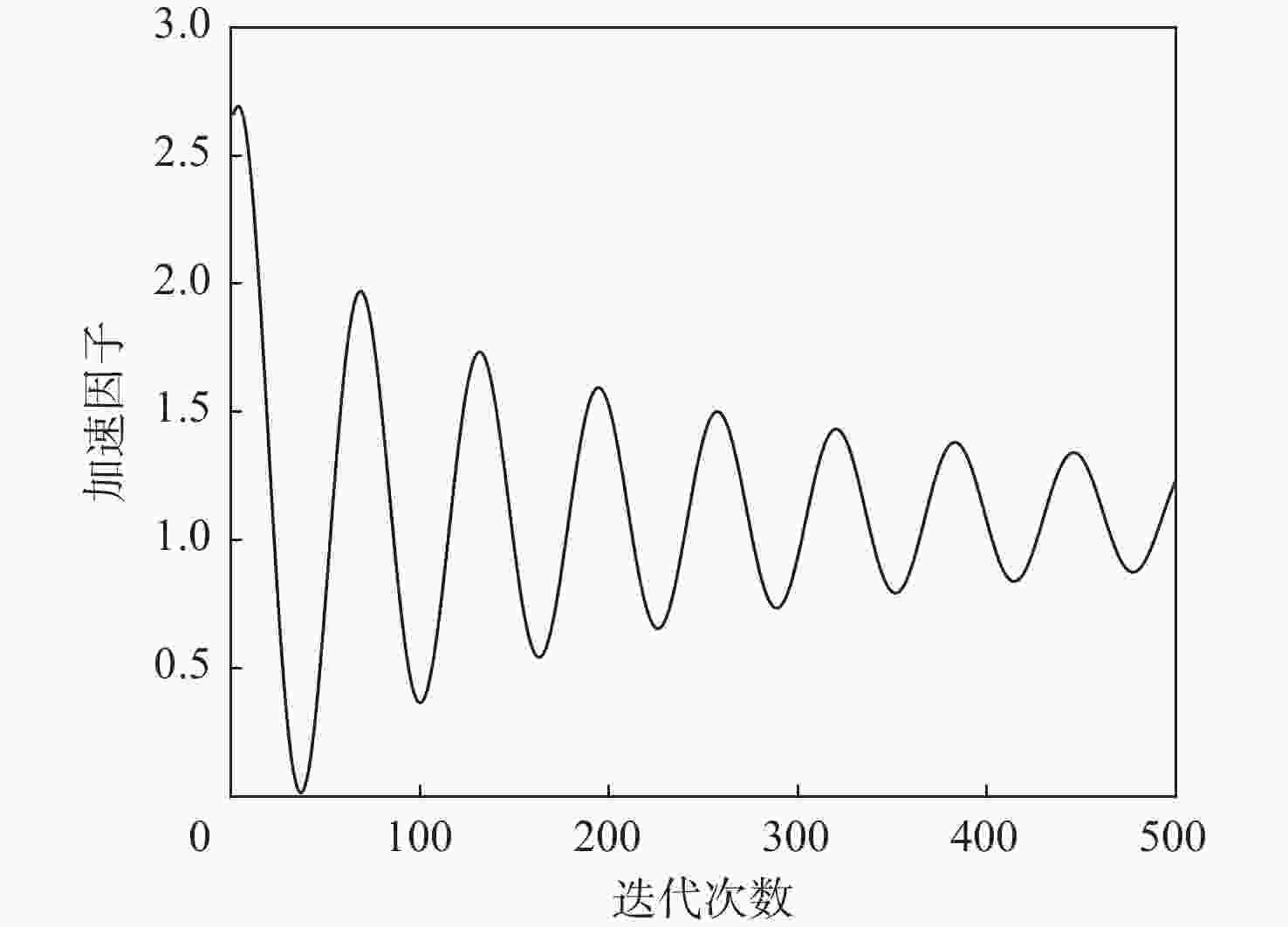
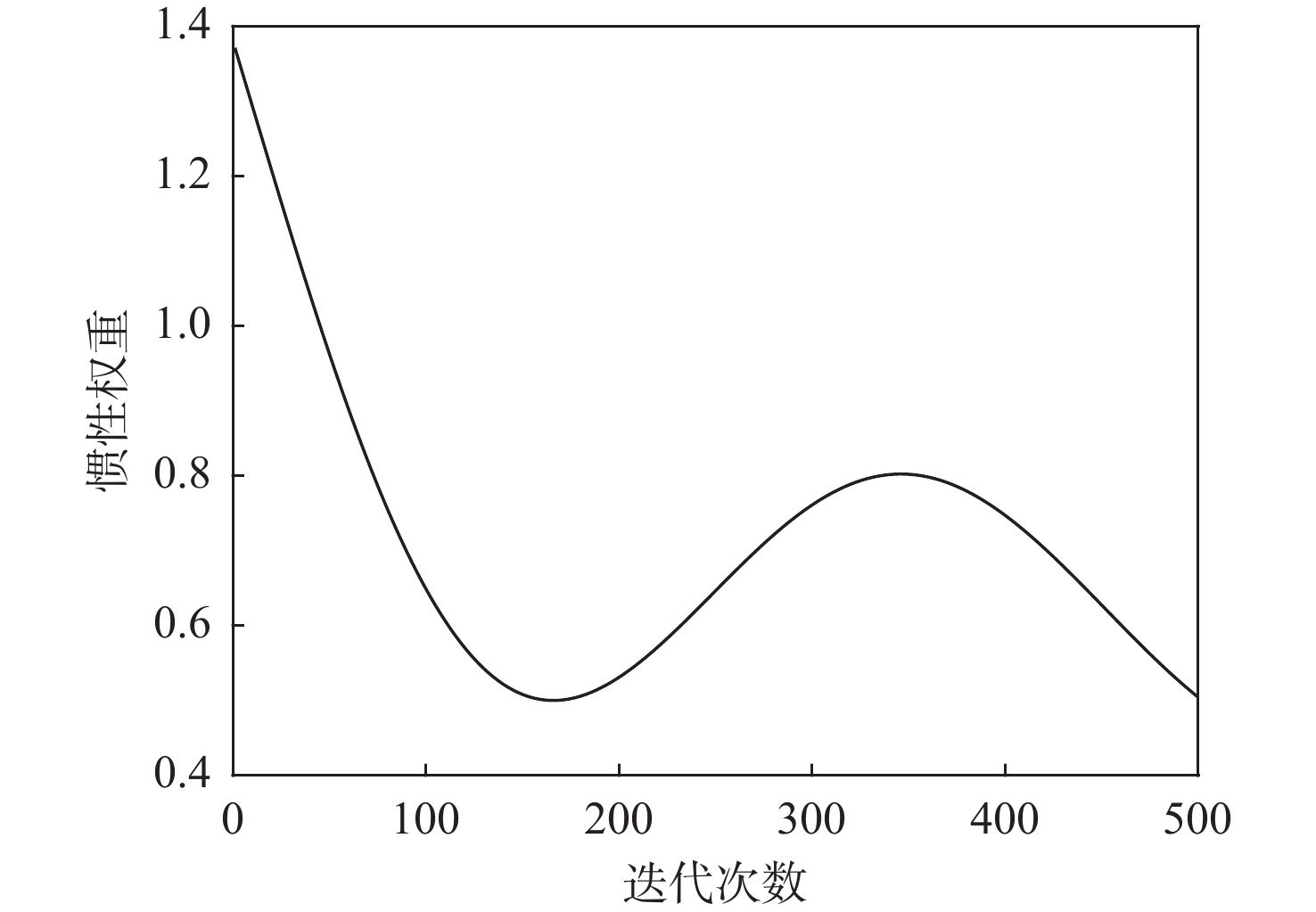
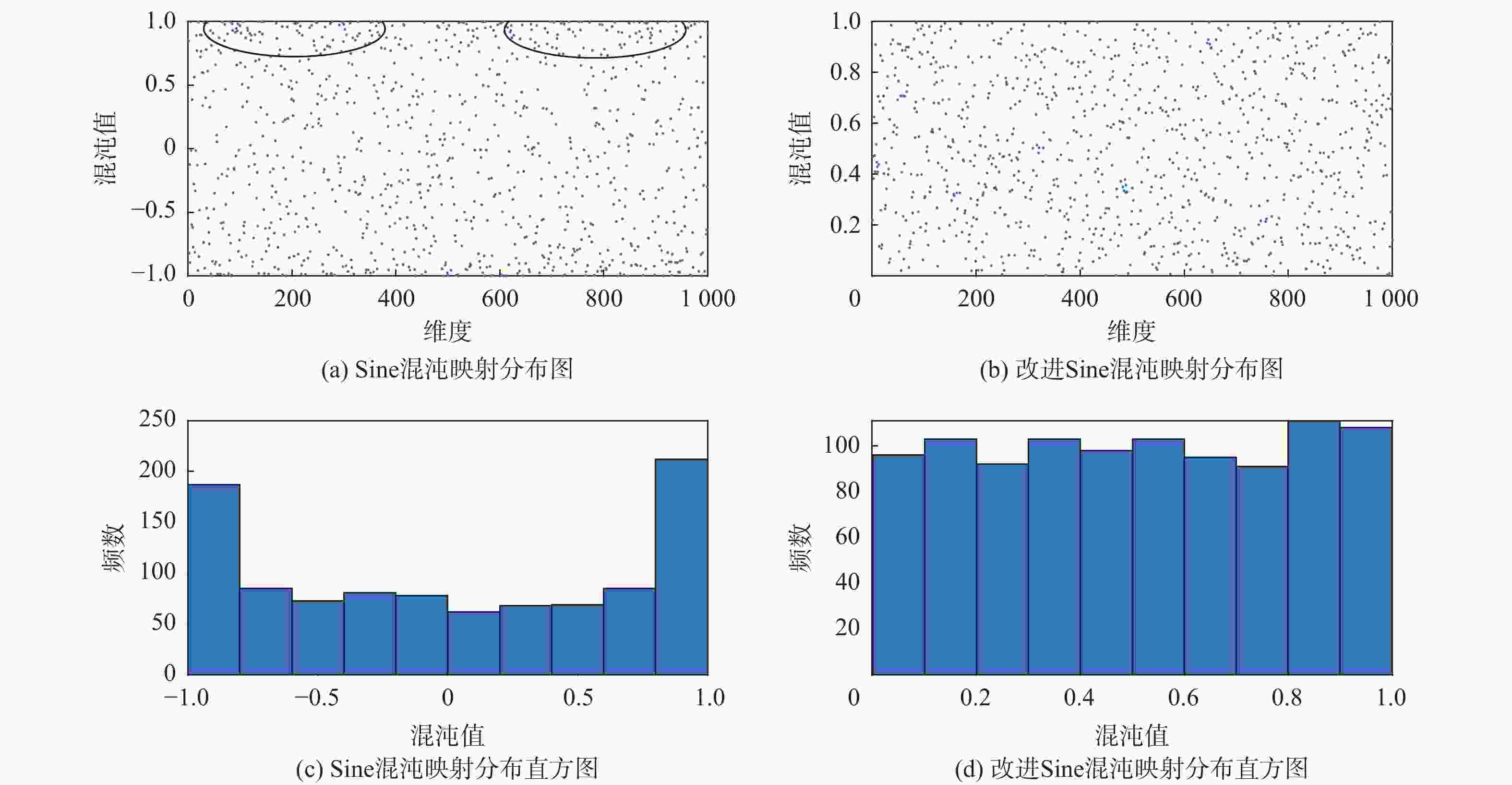
针对黑猩猩优化算法存在迭代速度慢、精度不高及初始化分布不均匀等问题，提出一种融合多策略的改进黑猩猩优化算法。采用改进的Sine混沌映射初始化种群，解决种群边界聚集分布问题，引入考虑线性权重系数、自适应加速因子的粒子群思想，配合改进的非线性收敛因子平衡算法的全局搜索能力，加快算法收敛，提高收敛精度。引入自适应水波因子改进麻雀精英突变和Bernoulli混沌映射策略，提高个体跳出局部最优的能力。利用22个基准测试函数进行迭代分析求解和Wilcoxon秩和统计检验，得出所提算法迭代速度更快、精度更高、跳出局部最优能力更强。将所提算法应用到工程实例中，进一步验证算法处理现实优化问题的优越性。
- 改进的Sine混沌映射 /
- 非线性衰减因子 /
- 麻雀精英突变 /
- Bernoulli混沌映射 /
- Wilcoxon秩和检验
Abstract:
In order to solve the problems of initial population boundary clustering distribution, slow convergence speed, low accuracy and easy falling into local optimum in chimpanzee search algorithm, an improved chimpanzee optimization algorithm with multi-strategy fusion (SPWChoA) was proposed. Firstly, the modified Sine chaotic map is used to initialize the population to solve the aggregation and distribution problem of population boundaries. Secondly, the concept of linear weight factor and adaptive acceleration factor for particle swarm optimization is presented. This is coupled with the enhanced nonlinear convergence factor balancing algorithm’s global search capability to quicken the algorithm’s convergence and raise its convergence accuracy. Finally, sparrow elite mutation and Bernoulli chaotic mapping strategies improved by adaptive water wave factors are introduced to improve the ability of individuals to jump out of local optima. By comparing the optimization results of 23 benchmark functions and Wilcoxon rank sum statistical test, it can be seen that the SPWChoA optimization algorithm has stronger robustness and applicability. Lastly, to further demonstrate the SPWChoA optimization algorithm’s superiority in handling actual optimization issues, the technique is applied to an engineering case.
- modified Sine chaotic mapping /
- nonlinear attenuation factor /
- sparrow elite mutation /
- Bernoulli chaotic mapping /
- Wilcoxon rank-sum test

HTML全文

图 1 混沌映射分布图和分布直方图

Figure 1. Distribution diagram and histogram of chaotic mapping

下载: 全尺寸图片幻灯片

图 2 加速因子变化曲线

Figure 2. Change curve of acceleration factor

下载: 全尺寸图片幻灯片

图 3 惯性权重变化曲线

Figure 3. Curve of inertia weight change

下载: 全尺寸图片幻灯片

图 4 收敛因子对比

Figure 4. Comparison of convergence factors

下载: 全尺寸图片幻灯片

图 5 500次迭代水波因子分布

Figure 5. Adaptive water wave factor distribution with 500 iterations

下载: 全尺寸图片幻灯片

图 6 本文算法优化流程

Figure 6. Flow chart of the proposed algrithm optimization

下载: 全尺寸图片幻灯片

图 7 连续单模态测试函数收敛曲线

Figure 7. Convergence curves for continuous single-modal test functions

下载: 全尺寸图片幻灯片

图 8 连续多模态测试函数收敛曲线

Figure 8. Convergence curves of continuous multi-modal test functions

下载: 全尺寸图片幻灯片

图 9 固定多模态测试函数收敛曲线

Figure 9. Convergence curves for fixed multi-modal test functions

下载: 全尺寸图片幻灯片

图 10 压力容器设计问题模型

Figure 10. Pressure vessel design problem model

下载: 全尺寸图片幻灯片

图 11 PID控制系统结构

Figure 11. Structure of PID control system

下载: 全尺寸图片幻灯片

图 12 500 MPa全自动活塞压力计

Figure 12. 500 MPa automatic piston manometer

下载: 全尺寸图片幻灯片

图 13 检定活塞位移曲线

Figure 13. Calibrate the piston displacement curve

下载: 全尺寸图片幻灯片

表 1 基准测试函数

Table 1. Benchmark functions

编号	函数名	定义域	维度	最优值	绝对精度误差
F₁	Sphere	[−100, 100]	30	0	1.00×10⁻³
F₂	Schwefel’ problem 2.22	[−10, 10]	30	0	1.00×10⁻³
F₃	Schwefel’ problem 1.2	[−100, 100]	30	0	1.00×10⁻³
F₄	Schwefel’ problem 2.21	[−100, 100]	30	0	1.00×10⁻³
F₅	Generalized Rosenbrock’s Function	[−30, 30]	30	0	1.00×10⁻²
F₆	Step Function	[−100, 100]	30	0	1.00×10⁻²
F₇	Quartic Function	[−1.28, 1.28]	30	0	1.00×10⁻²
F₈	Generalized Schwefel’s problem	[−500, 500]	30	−12569.5	1.00×10⁺⁰²
F₉	Generalized Rastrigin’s Function	[−5.12, 5.12]	30	0	1.00×10⁻²
F₁₀	Ackley’s Function	[−32, 32]	30	0	1.00×10⁻²
F₁₁	Ceneralized Criewank Function	[−600, 600]	30	0	1.00×10⁻²
F₁₂	Ceneralized Penalized Function	[−50, 50]	30	0	1.00×10⁻²
F₁₃	Ceneralized Penalized Function	[−50, 50]	30	0	1.00×10⁻²
F₁₄	Shekell’s Foxholes Function	[−65, 65]	2	1	1.00×10⁻²
F₁₅	Kowalik’s Function	[−5, 5]	4	0.0003	1.00×10⁻²
F₁₆	Six-Hump Camel-Back Function	[−5, 5]	2	−1.03	1.00×10⁻²
F₁₇	Branin Function	[−5, 5]	2	0.398	1.00×10⁻²
F₁₈	Goldstein-Price Function	[−2, 2]	2	3	1.00×10⁻²
F₁₉	Hatman’s Function1	[0, 1]	3	−3.86	1.00×10⁻²
F₂₀	Hatman’s Function2	[0, 1]	6	−3.32	1.00×10⁻²
F₂₁	Shekel’s Family 1	[0, 10]	4	−10	1.00×10⁻²
F₂₂	Shekel’s Family 2	[0, 10]	4	−10	1.00×10⁻²

下载: 导出CSV

表 2 函数测试实验结果（30维度）

Table 2. Experimental results of function test (30 dimensions)

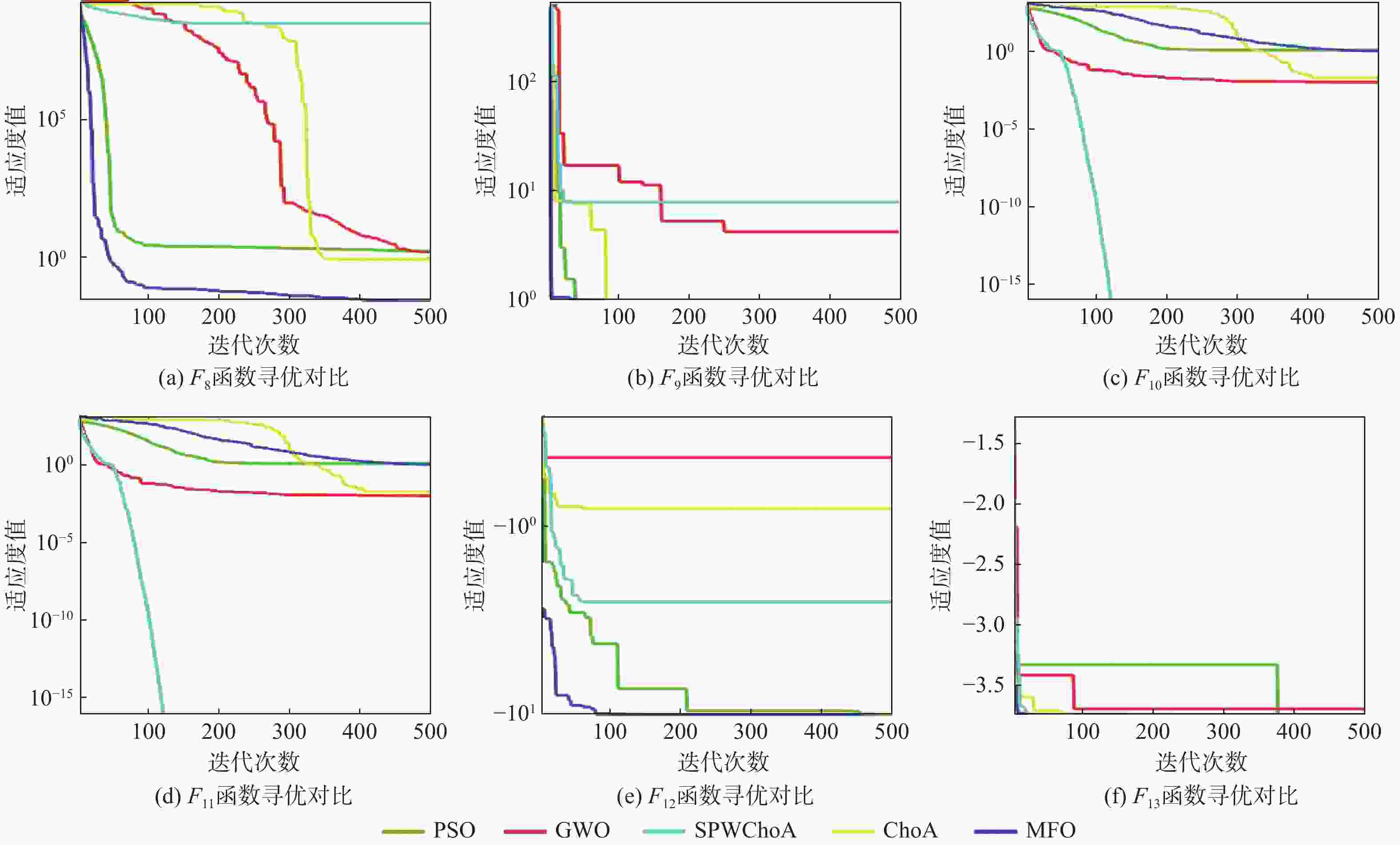
函数	算法	最优值	平均值	标准差
F₁	PSO	1.2781×10²	1.5311×10³	4.3431×10³
	GWO	2.0584×10⁻³¹	8.8881×10²	6.9157×10³
	本文算法	0	8.0417×10²	6.3995×10³
	ChoA	3.1555×10⁻⁷	5.2731×10⁴	4.8132×10⁴
	MFO	1.6961×10⁰	1.5902×10⁴	2.7030×10⁴
F₂	PSO	1.2720×10²	1.2561×10⁸	1.9841×10¹⁰
	GWO	3.2013×10⁻¹⁸	3.1168×10¹⁷	6.9157×10¹⁴
	本文算法	0	1.8601×10³	4.2861×10⁸
	ChoA	3.0828×10⁻⁶	3.5033×10¹¹	4.8132×10¹⁴
	MFO	2.1091×10¹	3.0726×10⁴	2.6503×10¹²
F₄	PSO	1.1627×10⁻¹	1.3258×10¹	7.7210×10⁰
	GWO	3.2850×10⁻⁵	9.5806×10⁰	2.5107×10¹
	本文算法	7.2961×10⁻²¹⁴	2.0326×10⁰	9.4542×10⁰
	ChoA	3.5794×10⁻⁰	6.4154×10¹	3.9189×10¹
	MFO	7.2761×10⁻¹	7.7294×10¹	6.2757×10¹
F₆	PSO	4.0547×10¹	1.1066×10³	6.8445×10³
	GWO	2.4012×10⁰	5.3471×10²	6.0318×10³
	本文算法	2.500×10⁻¹	6.2878×10²	5.3597×10³
	ChoA	4.0429×10⁰	4.9726×10⁴	4.7985×10⁴
	MFO	1.4837×10³	2.5441×10⁴	2.5183×10⁴
F₉	PSO	2.5862×10⁰	6.6511×10⁰	1.6784×10¹
	GWO	1.4830×10⁻³	1.8595×10⁰	2.1531×10¹
	本文算法	1.7312×10⁻⁴	1.0989×10⁰	1.3083×10¹
	ChoA	3.0276×10⁻⁴	6.7608×10¹	6.4684×10¹
	MFO	2.8249×10⁻¹	2.5109×10¹	5.4009×10¹
F₁₀	PSO	1.0908×10⁰	2.5820×10¹	8.9543×10¹
	GWO	0	8.1280×10¹	6.8696×10¹
	本文算法	0	9.9993×10¹	6.7406×10¹
	ChoA	4.8961×10⁻⁹	4.6463×10²	4.5693×10²
	MFO	9.6263×10¹	1.4153×10²	2.3021×10²
F₁₁	PSO	1.1879×10⁰	5.2039×10¹	1.2443×10²
	GWO	9.8189×10⁻³	9.1945×10⁰	6.8756×10¹
	本文算法	0	4.6855×10¹	4.5370×10¹
	ChoA	1.9166×10⁻²	3.6548×10²	3.4025×10²
	MFO	1.0202×10⁰	1.7967×10²	2.9490×10²
F₁₂	PSO	1.4136×10¹	1.3418×10⁶	1.9234×10⁷
	GWO	1.3312×10⁻¹	1.1371×10⁴	9.9317×10⁷
	本文算法	6.5778×10⁻³	7.5367×10⁵	7.6992×10⁶
	ChoA	8.7621×10⁻¹	4.3885×10⁸	4.2037×10⁷
	MFO	1.1178×10¹	2.6872×10⁷	9.2986×10⁷
F₁₈	PSO	3.0010×10⁰	4.5238×10⁰	1.4169×10¹
	GWO	3.0101×10⁰	1.2183×10⁰	1.2183×10¹
	本文算法	3.0000×10⁰	3.116×10⁰	3.1160×10⁰
	ChoA	3.1003×10⁰	4.3993×10⁰	4.3993×10⁰
	MFO	3.0503×10⁰	2.2443×10¹	1.7656×10¹
F₁₉	PSO	−3.8628×10⁰	−3.8579×10⁻⁰	2.3883×10⁻²
	GWO	−3.8527×10⁰	−3.6856×10⁰	6.6644×10¹
	本文算法	−3.9857×10⁰	−3.9856×10⁰	2.6140×10⁻³
	ChoA	−3.8542×10⁰	−3.7941×10⁰	1.6723×10⁻¹
	MFO	−3.8628×10⁰	−3.8348×10⁰	2.0741×10⁻¹
F₂₀	PSO	−3.3220×10⁰	−3.2669×10⁰	2.3233×10⁻¹
	GWO	−3.2006×10⁰	−3.1586×10⁰	2.0946×10⁻¹
	本文算法	−3.8518×10⁰	−3.8516×10⁰	2.0518×10⁻⁴
	ChoA	−3.0137×10⁰	−2.7966×10⁰	5.0789×10⁻¹
	MFO	−3.2031×10⁰	−3.1805×10⁰	1.5436×10⁻¹
F₂₁	PSO	−2.6305×10⁰	−2.5943×10⁻⁰	2.1477×10⁻¹
	GWO	−4.2547×10⁻¹	−4.2544×10⁻¹	3.2649×10⁰
	本文算法	−1.0153×10¹	−6.6549×10⁰	7.3892×10⁻⁴
	ChoA	−4.9728×10⁻¹	−4.9222×10⁻¹	2.3510×10⁻²
	MFO	−5.0552×10⁰	−4.8147×10⁰	9.3764×10⁻¹
F₂₂	PSO	−6.3216×10⁻¹	−6.3212×10⁻¹	5.5567×10⁻¹⁶
	GWO	−3.7308×10⁻¹	−3.7308×10⁻¹	3.6373×10⁻¹
	本文算法	−5.0877×10⁰	−4.9420×10⁻¹	2.672×10⁻¹⁶
	ChoA	−4.9733×10⁰	−2.1872×10⁻¹	1.9431×10⁰
	MFO	−5.0877×10⁰	−4.8186×10⁻¹	9.6067×10⁻¹

下载: 导出CSV

表 3 Wilcoxon 秩和检验结果

Table 3. Wilcoxon rank-sum test results

函数	PSO	GWO	ChoA	MFO
F₁	3.01×10⁻²⁰	3.01×10⁻²⁰	3.01×10⁻²⁰	3.01×10⁻²⁰
F₂	3.01×10⁻²⁰	3.01×10⁻²⁰	3.01×10⁻²⁰	3.01×10⁻²⁰
F₃	3.01×10⁻²⁰	3.01×10⁻²⁰	3.01×10⁻²⁰	3.01×10⁻²⁰
F₄	3.01×10⁻²⁰	3.01×10⁻²⁰	3.01×10⁻²⁰	3.01×10⁻²⁰
F₅	1.28×10⁻¹⁷	2.66×10⁻¹⁷	2.29×10⁻¹⁰	1.04×10⁻¹⁰
F₆	7.21×10⁻¹⁸	7.07×10⁻¹⁸	1.36×10⁻¹⁷	1.38×10⁻¹⁰
F₇	3.41×10⁻²⁰	3.31×10⁻²⁰	1.21×10⁻¹⁹	NaN
F₈	3.41×10⁻²⁰	3.31×10⁻²⁰	2.96×10⁻²⁰	2.39×10⁻¹⁶
注：NaN表示无限大。

下载: 导出CSV

表 4 压力容器设计问题中各算法的最优解

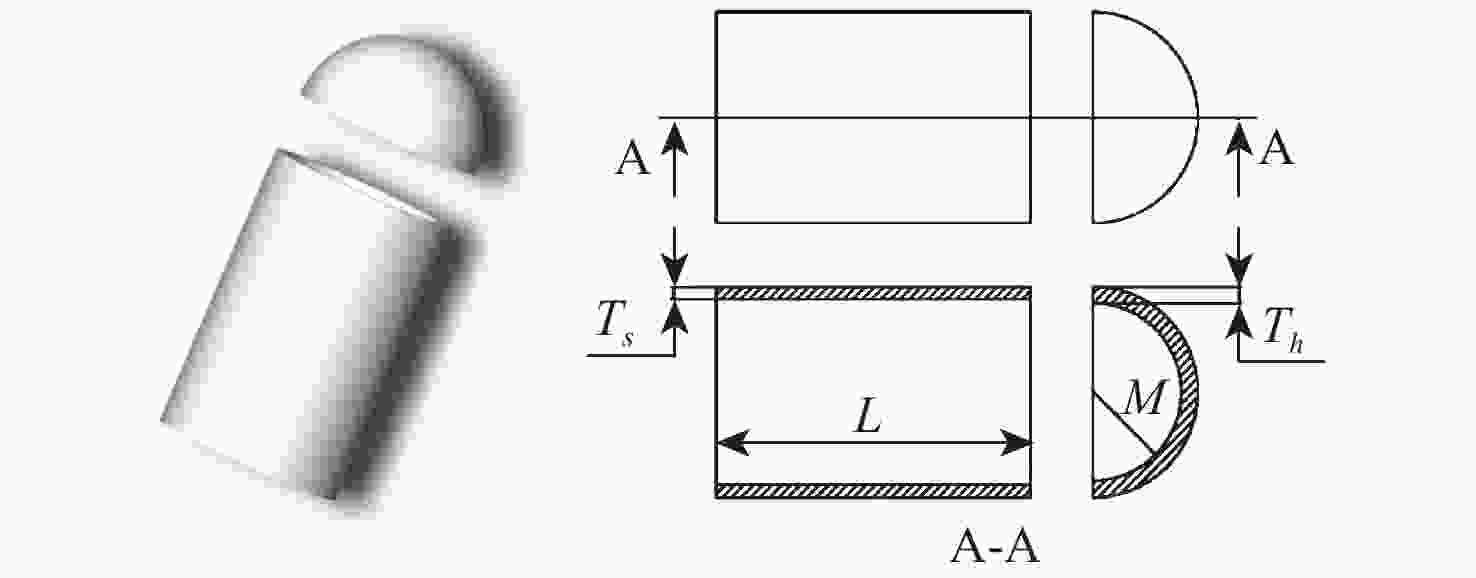
Table 4. Optimal solutions of each algorithm in pressure vessel design problem

算法	T_s	T_h	M	L	适应度值
PSO	1.9841	0.8452	69.1476	84.1523	14321.1522
GWO	2.1425	0.7854	78.1463	63.1789	9542.1896
本文算法	1.2454	0.4251	65.1789	54.3254	7854.2547
ChoA	1.5748	0.8745	78.1245	66.1385	9854.1245
MFO	1.8254	0.5623	49.1278	78.3569	12412.1247

下载: 导出CSV

表 5 不同算法优化PID控制器得出的整定参数

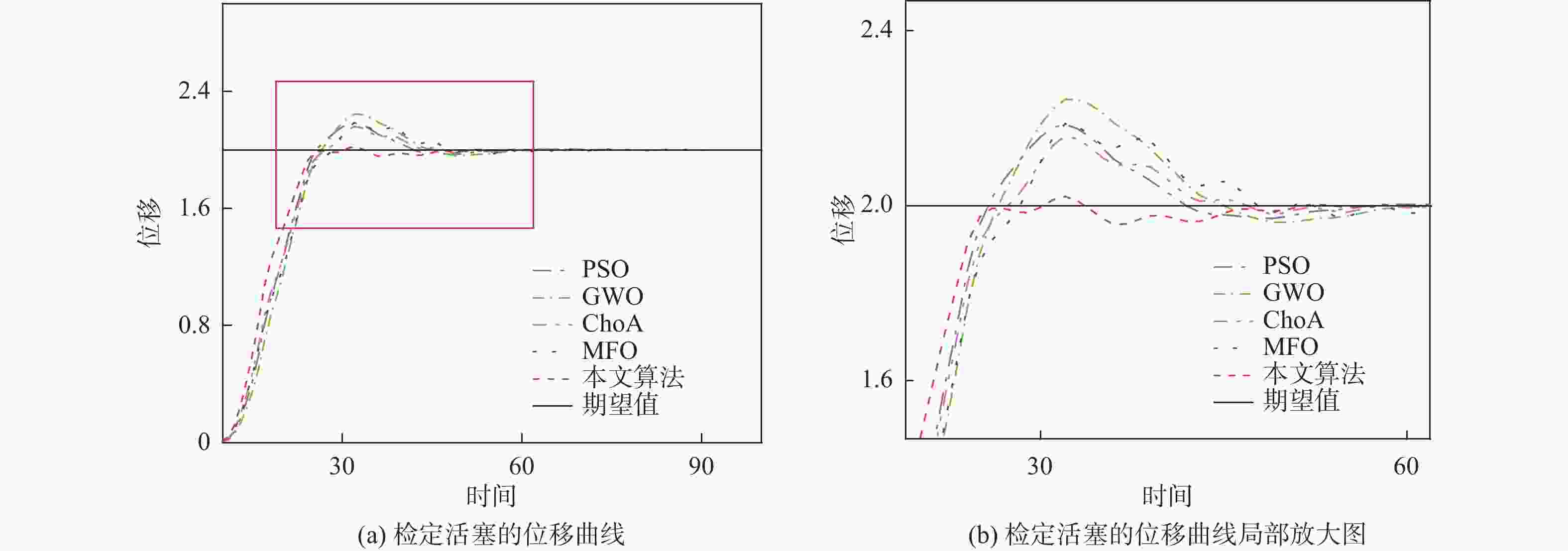
Table 5. Tuning parameters derived from PID controller optimized by different algorithms

算法	K_p	K_i	K_d	适应度值
PSO	0.6653	0.7324	0.6614	65.4575
GWO	0.7854	0.5875	0.2221	78.1245
SPWChoA	0.2877	0.0478	0.8574	33.4578
ChoA	0.7841	0.7854	0.7541	63.1451
MFO	0.7533	0.3751	0.5315	77.5541

下载: 导出CSV

参考文献(24)

[1]	卢纯义, 于津, 余忠东, 等. 基于改进灰狼算法优化SVR的混凝土中钢筋直径检测方法[J]. 计算机科学, 2022, 49(11): 228-233. doi: 10.11896/jsjkx.210800039 LU C Y, YU J, YU Z D, et al. Detection method of rebar in concrete diameter based on improved grey wolf optimizer-based SVR[J]. Computer Science, 2022, 49(11): 228-233(in Chinese). doi: 10.11896/jsjkx.210800039
[2]	于振华, 刘争气, 刘颖, 等. 基于自适应混合粒子群优化的软件缺陷预测特征选择方法[J]. 计算机应用, 2023, 43(4): 1206-1213. doi: 10.11772/j.issn.1001-9081.2022030444 YU Z H, LIU Z Q, LIU Y, et al. Feature selection method based on self-adaptive hybrid particle swarm optimization for software defect prediction[J]. Journal of Computer Applications, 2023, 43(4): 1206-1213(in Chinese). doi: 10.11772/j.issn.1001-9081.2022030444
[3]	张可为, 赵晓林, 何利, 等. 一种改进X-best引导个体和动态等级更新机制的鸡群算法[J]. 北京麻豆精品秘国产传媒学报, 2021, 47(12): 2579-2593. ZHANG K W, ZHAO X L, HE L, et al. A chicken swarm optimization algorithm based on improved X-best guided individual and dynamic hierarchy update mechanism[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(12): 2579-2593(in Chinese).
[4]	郑旸, 龙英文, 吉明明, 等. 融合螺旋黏菌算法的混沌麻雀搜索算法与应用[J]. 计算机工程与应用, 2023, 59(14): 124-133. doi: 10.3778/j.issn.1002-8331.2204-0073 ZHENG Y, LONG Y W, JI M M, et al. Chaotic sparrow search algorithm and application based on spiral slime mould algorithm[J]. Computer Engineering and Applications, 2023, 59(14): 124-133(in Chinese). doi: 10.3778/j.issn.1002-8331.2204-0073
[5]	THARWAT A, ELHOSENY M, HASSANIEN A E, et al. Intelligent Bézier curve-based path planning model using chaotic particle swarm optimization algorithm[J]. Cluster Computing, 2019, 22(2): 4745-4766.
[6]	王一镜, 罗广恩, 王陈阳, 等. 基于自适应变异粒子群算法的船舶结构优化方法[J]. 中国舰船研究, 2022, 17(2): 156-164. WANG Y J, LUO G E, WANG C Y, et al. Ship structural optimization method based on daptive mutation particle swarm algorithm[J]. Chinese Journal of Ship Research, 2022, 17(2): 156-164(in Chinese).
[7]	缪燕子, 王玥, 李元龙, 等. 融合学习策略与导向果蝇机制的气味源主动定位方法研究[J]. 控制理论与应用, 2023, 40(5): 913-922. doi: 10.7641/CTA.2022.11078 MIAO Y Z, WANG Y, LI Y L, et al. Study on active odor source localization method based on learning strategy and guided fruit fly mechanism[J]. Control Theory & Applications, 2023, 40(5): 913-922(in Chinese). doi: 10.7641/CTA.2022.11078
[8]	LU C, GAO L, YI J. Grey wolf optimizer with cellular topological structure[J]. Expert Systems with Applications, 2018, 107: 89-114. doi: 10.1016/j.eswa.2018.04.012
[9]	王子恺, 黄学雨, 朱东林, 等. 融合边界处理机制的学习型麻雀搜索算法[J]. 北京麻豆精品秘国产传媒学报, 2024, 50(1): 286-298. WANG Z K, HUANG X Y, ZHU D L, et al. Learning sparrow search algorithm of hybrids boundary processing mechanisms[J]. Journal of Beijing University of Aeronautics and Astronautics, 2024, 50(1): 286-298(in Chinese).
[10]	王万良, 金雅文, 陈嘉诚, 等. 多角色多策略多目标粒子群优化算法[J]. 浙江大学学报(工学版), 2022, 56(3): 531-541. doi: 10.3785/j.issn.1008-973X.2022.03.012 WANG W L, JIN Y W, CHEN J C, et al. Multi role multi strategy multi-objective particle swarm optimization algorithm[J]. Journal of Zhejiang University (Engineering Science), 2022, 56(3): 531-541(in Chinese). doi: 10.3785/j.issn.1008-973X.2022.03.012
[11]	张晶, 贺媛媛. 融合正余弦优化与跳距优化的DV-Hop定位算法[J]. 计算机工程与科学, 2022, 44(4): 645-653. doi: 10.3969/j.issn.1007-130X.2022.04.008 ZHANG J, HE Y Y. A DV-Hop positioning algorithm combining sine and cosine optimization and hop distance optimization[J]. Computer Engineering & Science, 2022, 44(4): 645-653(in Chinese). doi: 10.3969/j.issn.1007-130X.2022.04.008
[12]	李爱莲, 全凌翔, 崔桂梅, 等. 融合正余弦和柯西变异的麻雀搜索算法[J]. 计算机工程与应用, 2022, 58(3): 91-99. doi: 10.3778/j.issn.1002-8331.2106-0148 LI A L, QUAN L X, CUI G M, et al. Sparrow search algorithm combining sine-cosine and Cauchy mutation[J]. Computer Engineering and Applications, 2022, 58(3): 91-99(in Chinese). doi: 10.3778/j.issn.1002-8331.2106-0148
[13]	谭慧娟, 李世明, 郭文鑫, 等. 基于混沌自适应人工鱼群算法的含家庭储能配电网快速重构方法[J]. 太阳能学报, 2022, 43(5): 468-477. TAN H J, LI S M, GUO W X, et al. Fast reconfiguration method of distribution network with household energy storage based on chaotic adaptive artificial fish swarm algorithm[J]. Acta Energiae Solaris Sinica, 2022, 43(5): 468-477(in Chinese).
[14]	吕鑫, 慕晓冬, 张钧, 等. 混沌麻雀搜索优化算法[J]. 北京麻豆精品秘国产传媒学报, 2021, 47(8): 1712-1720. LU X, MU X D, ZHANG J, et al. Chaos sparrow search optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(8): 1712-1720(in Chinese).
[15]	SAYED S A F, NABIL E, BADR A. A binary clonal flower pollination algorithm for feature selection[J]. Pattern Recognition Letters, 2016, 77: 21-27. doi: 10.1016/j.patrec.2016.03.014
[16]	刘成汉, 何庆. 融合多策略的黄金正弦黑猩猩优化算法[J]. 自动化学报, 2023, 49(11): 2360-2373. LIU C H, HE Q. Golden sine chimp optimization algorithm integrating multiple strategies[J]. Acta Automatica Sinica, 2023, 49(11): 2360-2373(in Chinese).
[17]	滕志军, 吕金玲, 郭力文, 等. 一种基于Tent映射的混合灰狼优化的改进算法[J]. 哈尔滨工业大学学报, 2018, 50(11): 40-49. doi: 10.11918/j.issn.0367-6234.201806096 TENG Z J, LV J L, GUO L W, et al. An improved hybrid grey wolf optimization algorithm based on Tent mapping[J]. Journal of Harbin Institute of Technology, 2018, 50(11): 40-49(in Chinese). doi: 10.11918/j.issn.0367-6234.201806096
[18]	王鹏飞, 杜忠华, 牛坤, 等. 基于改进粒子群算法的倒立摆LQR优化控制[J]. 计算机仿真, 2021, 38(2): 220-224. doi: 10.3969/j.issn.1006-9348.2021.02.048 WANG P F, DU Z H, NIU K, et al. LQR optimal control of inverted pendulum based on improved particle swarm optimization algorithm[J]. Computer Simulation, 2021, 38(2): 220-224(in Chinese). doi: 10.3969/j.issn.1006-9348.2021.02.048
[19]	唐延强, 李成海, 宋亚飞, 等. 自适应变异麻雀搜索优化算法[J]. 北京麻豆精品秘国产传媒学报, 2023, 49(3): 681-692. TANG Y Q, LI C H, SONG Y F, et al. Adaptive mutation sparrow search optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(3): 681-692(in Chinese).
[20]	何庆, 罗仕杭. 混合改进策略的黑猩猩优化算法及其机械应用[J]. 控制与决策, 2023, 38(2): 354-364. HE Q, LUO S H. Hybrid improved chimpanzee optimization algorithm and its mechanical application[J]. Control and Decision, 2023, 38(2): 354-364(in Chinese).
[21]	刘景森, 袁蒙蒙, 左方. 面向全局搜索的自适应领导者樽海鞘群算法[J]. 控制与决策, 2021, 36(9): 2152-2160. LIU J S, YUAN M M, ZUO F. Global search-oriented adaptive leader salp swarm algorithm[J]. Control and Decision, 2021, 36(9): 2152-2160(in Chinese).
[22]	汪超, 王丙柱, 岑豫皖, 等. 基于多样性全局最优引导和反向学习的离子运动算法[J]. 控制与决策, 2020, 35(7): 1584-1596. WANG C, WANG B Z, CEN Y W, et al. Ions motion optimization algorithm based on diversity optimal guidance and opposition-based learning[J]. Control and Decision, 2020, 35(7): 1584-1596(in Chinese).
[23]	DERRAC J, GARCÍA S, MOLINA D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3-18. doi: 10.1016/j.swevo.2011.02.002
[24]	张新明, 王霞, 康强. 改进的灰狼优化算法及其高维函数和FCM优化[J]. 控制与决策, 2019, 34(10): 2073-2084. ZHANG X M, WANG X, KANG Q. Improved grey wolf optimizer and its application to high dimension function and FCM optimization[J]. Control and Decision, 2019, 34(10): 2073-2084(in Chinese).