Evolutionary game of subsidy strategy on multi-airport route network under homogeneous competition
-
摘要:
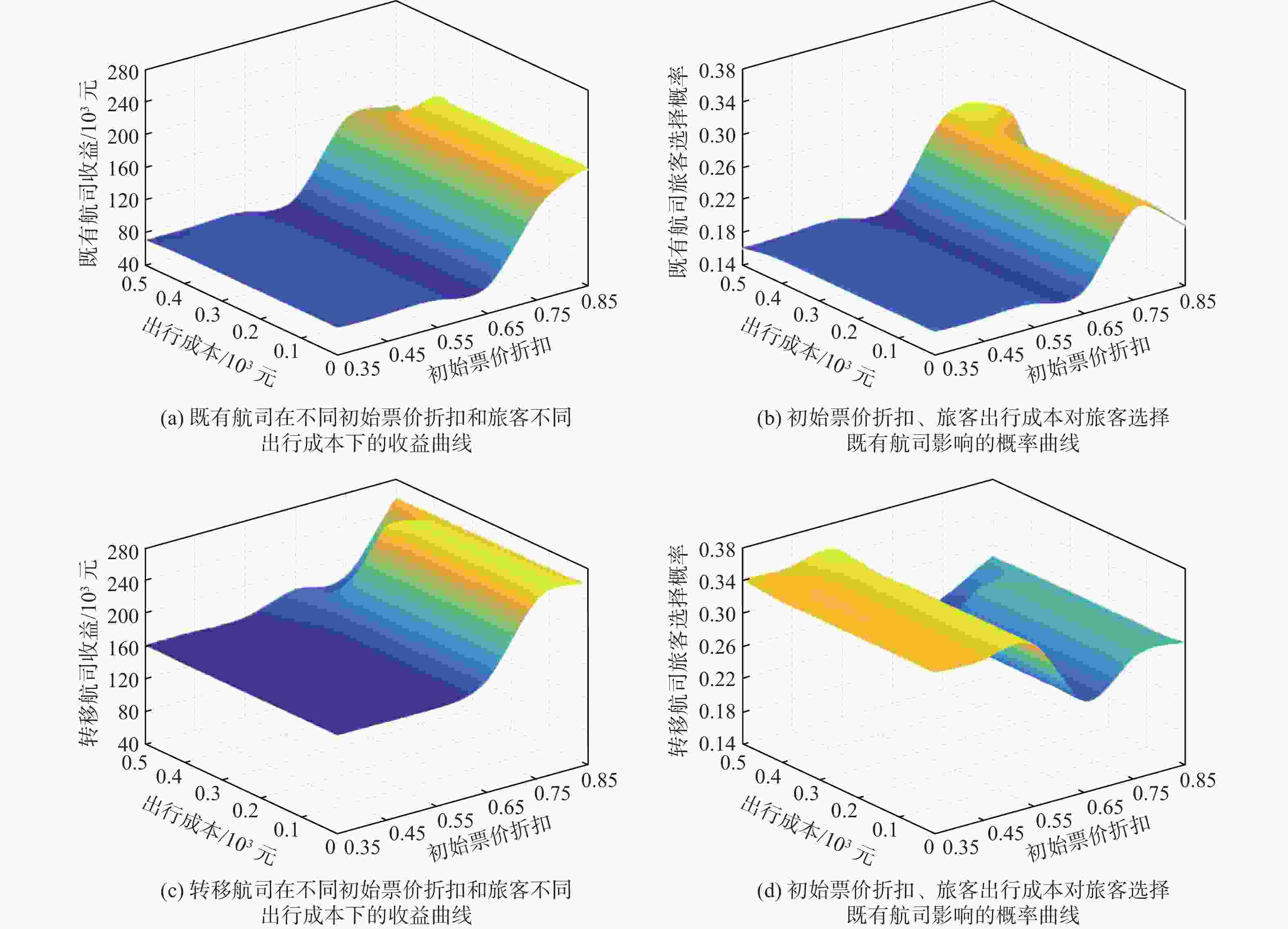
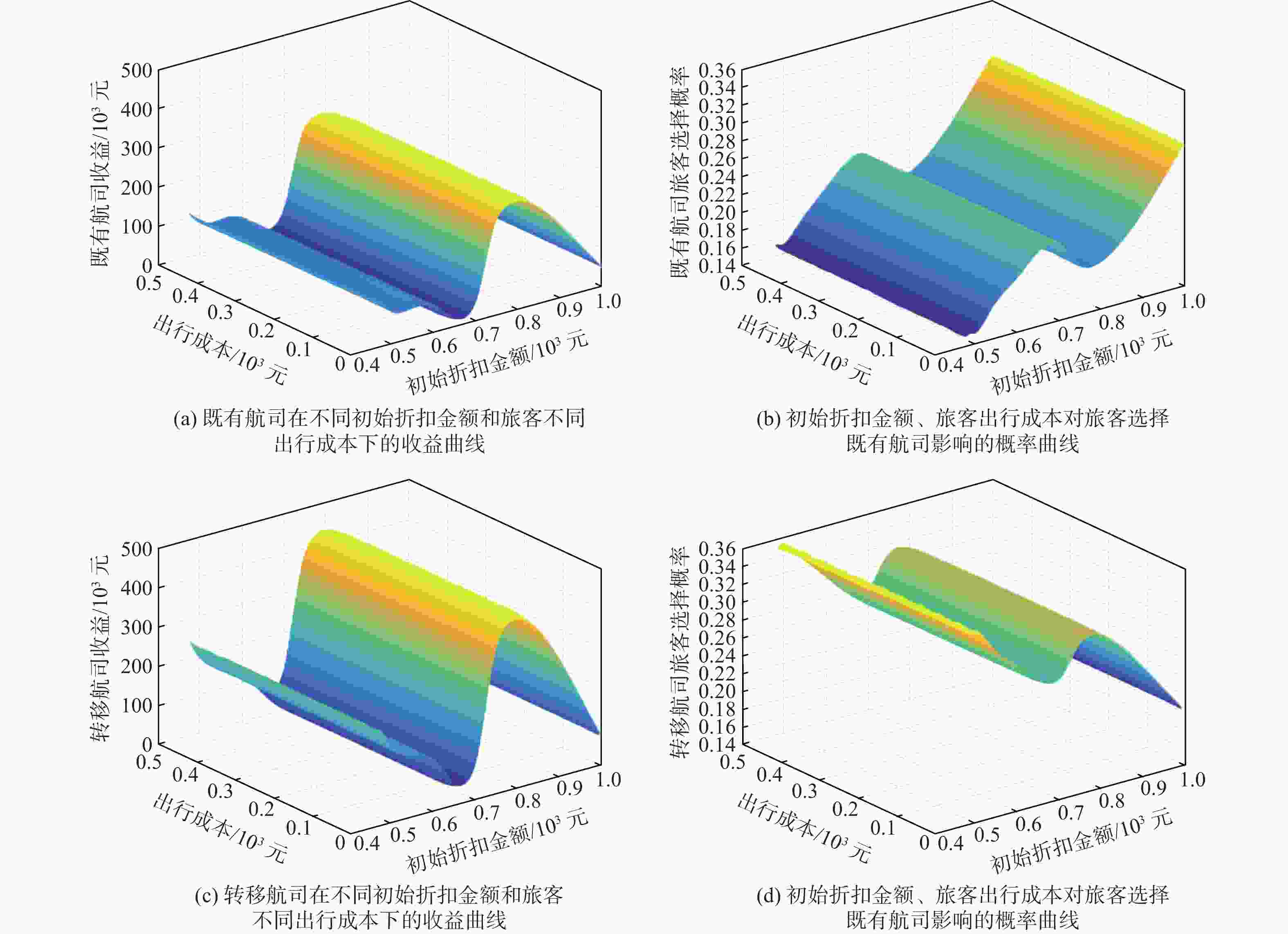
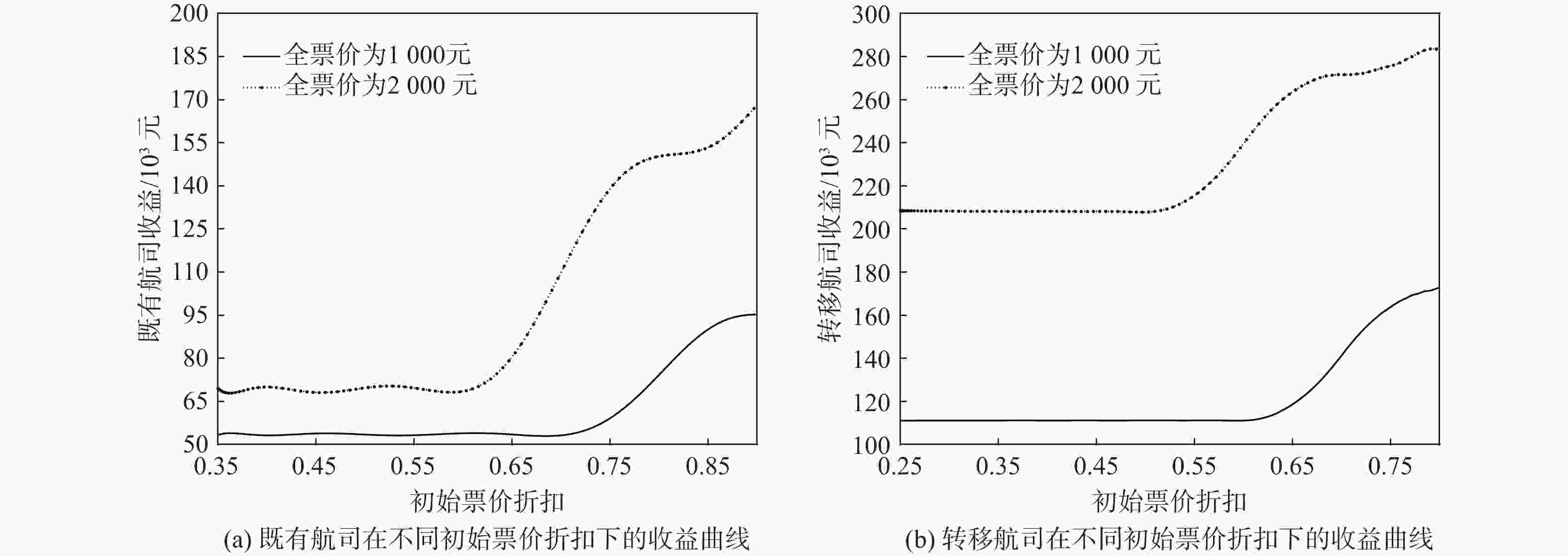
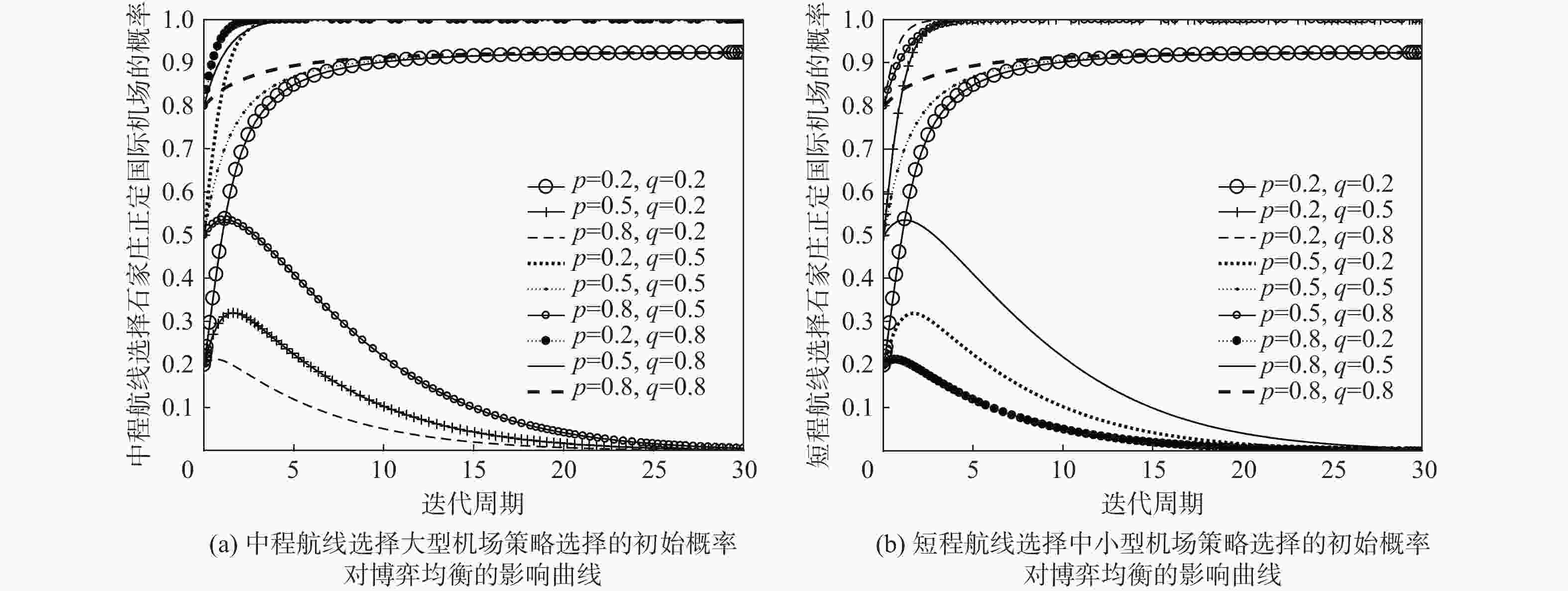
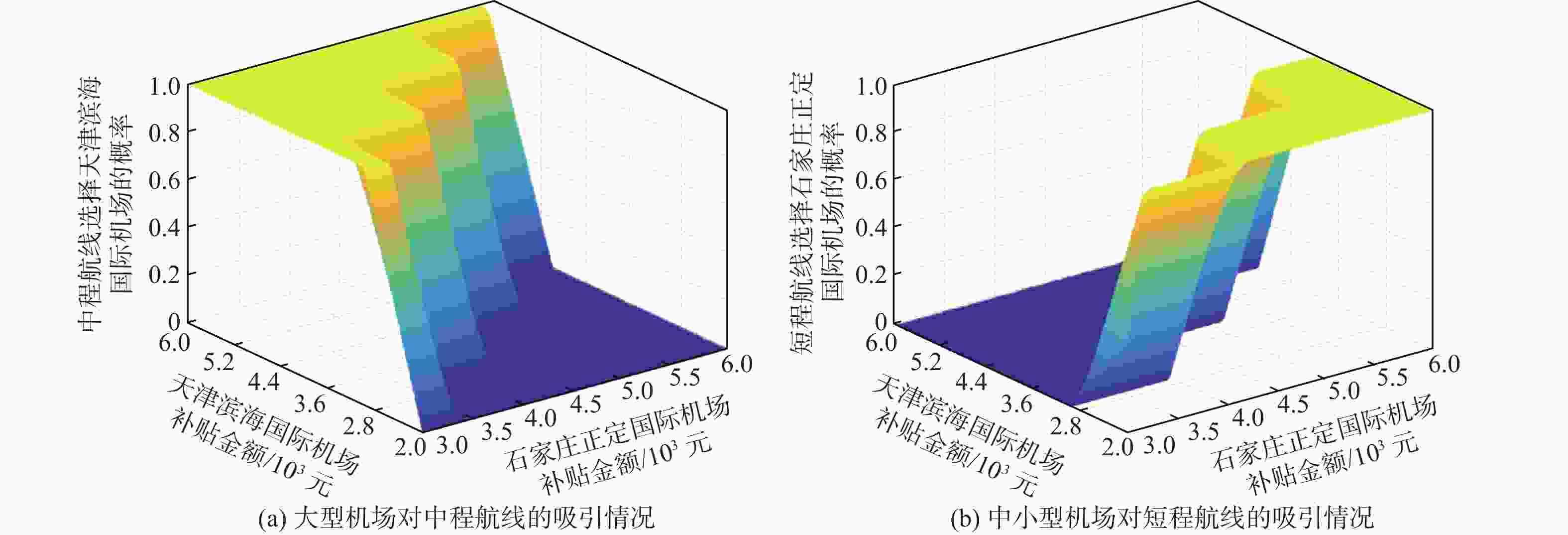
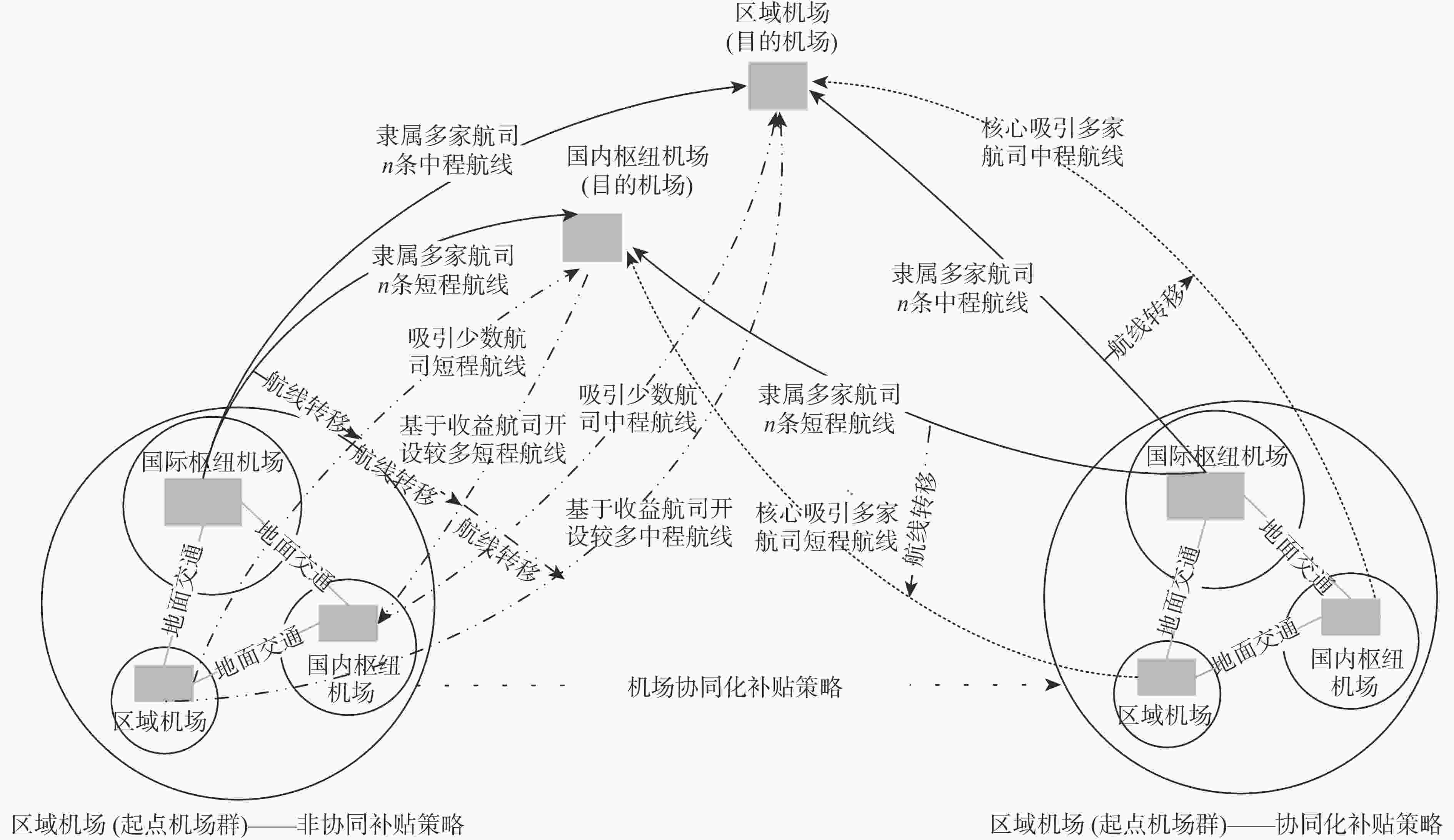
为实现区域内多机场基于差异化定位的高质量协同发展，研究机场差异化补贴策略对多机场航线网络演化影响，进而确定最佳补贴策略。基于旅客、航司、机场间的竞争博弈关系，构建了双层演化博弈模型。在上层博弈模型中，考虑旅客自学能力对票价的影响，构建融合自学习机制的Logit旅客选择模型，利用Hotelling定价模型分析同一航线航司间票价竞争对旅客选择行为的影响，进而确定在竞争条件下航司最佳定价策略；在下层博弈模型中，基于复制动态方程分析各机场补贴与航司间竞争性选择航线优化过程，确定机场间协同补贴策略与航线网络协同效果。结果表明：对于转移航线的航司，吸引“渗流”旅客的优势票价折扣区间为0.6～0.75；同航线竞争的航司票价折扣集中在0.6～0.85之间，可避免出现低价竞争带来的收益共损；通过机场差异化补贴实现航线网络优化，不同机场均存在基于差异化功能定位的最佳补贴区间。
Abstract:To enhance the high-quality collaborative development of multiple airports in the region based on differentiated positioning, the impact of airport subsidy strategies on the evolution of the multi-airport route network was studied, and the optimal subsidy strategy was determined. A double-layer evolutionary game model was constructed based on the competitive game relationships among passengers, airlines, and airports. In the upper-level model, the influence of passengers’ self-learning ability on fares was considered, and a passenger Logit choice model incorporating a self-learning mechanism was constructed. The Hotelling model was then used to analyze the impact of fare competition among airlines on the same route on passenger choice behavior, thereby determining the optimal pricing strategy for airlines under competitive conditions. In the lower-level model, the evolutionary game process of competitive choices between airport subsidies and airlines was analyzed based on the replicator dynamic equation. The synergistic effect of the inter-airport collaborative subsidy strategy and the route network was determined.The results show that for airlines transferring routes, the advantageous discount range for attracting leakage passengers is between 0.6 and 0.75. The fare discounts for airlines competing on the same route should be concentrated between 0.6 and 0.85 to avoid the loss of revenue caused by low price competition. Additionally, the optimization of the route network through airport subsidies reveals that each airport has an optimal subsidy range based on its functional positioning.
-
图 1 机场间航线网络协同演化示意图
Figure 1. Collaborative evolution diagram of route network between airports
图 3 航司初始票价折扣与收益、旅客选择概率关系
Figure 3. The relationship between initial ticket price discount and revenue, passenger selection probability of airlines
图 4 航司初始折扣金额与收益、旅客选择概率关系
Figure 4. The relationship between initial discount amount of airlines and revenue, passenger selection probability
图 6 策略选择的初始概率对演化博弈的影响
Figure 6. The impact of initial probability of strategy selection on evolutionary games
图 7 待转移航线系数对演化博弈的影响
Figure 7. The impact of pending transfer route coefficient on evolutionary games
表 1 基于出行策略的旅客效益矩阵
Table 1. Passenger benefit matrix based on travel strategy
策略种类 旅客$ i $效益 旅客$ j $效益 渗流与渗流 $ \overline A \left( t \right) + G $ $ \overline A \left( t \right) + G $ 渗流与非渗流 $ \overline A \left( t \right) + G $ $ {A^ * } + Q $ 非渗流与渗流 $ {A^ * } + Q $ $ \overline A \left( t \right) + G $ 非渗流与非渗流 $ {A^ * } + Q $ $ {A^ * } + Q $ 
下载: 导出CSV
表 2 航司转移策略效用矩阵
Table 2. Utility matrix of airline transfer strategies
策略种类 航司$ R $优化中程航线 航司$ R $优化短程航线 中小机场至中小机场 $ \varPi _R^{g = 1} + \delta S_R^{g = 1} - D_R^{g = 1} - {L_R} - {I^{g = 1}} $ $ \tilde \varPi _R^{g = 1} + \delta \tilde S_R^{g = 1} - \tilde D_R^{g = 1} - {\tilde L_R} - {I^{g = 1}} $ 中小机场至大型机场 $ \varPi _R^{g = 1} + S_R^{g = 1} - D_R^{g = 1} - {L_R} - {I^{g = 1}} $ $ \tilde \varPi _R^{g = 2} + \tilde S_R^{g = 2} - \tilde D_R^{g = 2} - {\tilde L_R} - {I^{g = 2}} $ 大型机场至中小机场 $ \varPi _R^{g = 2} + S_R^{g = 2} - D_R^{g = 2} - {L_R} - {I^{g = 2}} $ $ \tilde \varPi _R^{g = 1} + \tilde S_R^{g = 1} - \tilde D_R^{g = 1} - {\tilde L_R} - {I^{g = 1}} $ 大型机场至大型机场 $ \varPi _R^{g = 2} + \delta S_R^{g = 2} - D_R^{g = 2} - {L_R} - {I^{g = 2}} $ $ \tilde \varPi _R^{g = 2} + \delta \tilde S_R^{g = 2} - \tilde D_R^{g = 2} - {\tilde L_R} - {I^{g = 2}} $
下载: 导出CSV
表 3 均衡点的稳定性分析
Table 3. Stability analysis of equilibrium points
均衡解 特征值 稳定性 $ \left( {0,0} \right) $ $ \Delta {\varPi _R} - \Delta {D_R} - \Delta I + S_R^{g = 1} - \delta S_R^{g = 2} $
$ \Delta {\tilde \varPi _R} - \Delta {\tilde D_R} - \Delta I + \tilde S_R^{g = 1} - \delta \tilde S_R^{g = 2} $不确定 $ \left( {0,1} \right) $ $ \Delta {\varPi _R} - \Delta {D_R} - \Delta I - S_R^{g = 2} + \delta S_R^{g = 1} $
$ - \Delta {\tilde \varPi _R} + \Delta {\tilde D_R} + \Delta I + \tilde S_R^{g = 2} - \delta \tilde S_R^{g = 1} $不确定 $ \left( {1,0} \right) $ $ - \Delta {\varPi _R} + \Delta {D_R} + \Delta I - S_R^{g = 1} + \delta S_R^{g = 2} $
$ \Delta {\tilde \varPi _R} - \Delta {\tilde D_R} - \Delta I + \tilde S_R^{g = 1} - \delta \tilde S_R^{g = 2} $不确定 $ \left( {1,1} \right) $ $ - \Delta {\varPi _R} + \Delta {D_R} + \Delta I + S_R^{g = 2} - \delta S_R^{g = 1} $
$ - \Delta {\tilde \varPi _R} + \Delta {\tilde D_R} + \Delta I + \tilde S_R^{g = 2} - \delta \tilde S_R^{g = 1} $不确定 $ \left( {{p^ * },{q^ * }} \right) $ $ {\varOmega _1} $
$ {\varOmega _2} $不确定
下载: 导出CSV
表 4 上层博弈模型初值设置
Table 4. Initial value setting of upper level game model
参数 参数
基准值变化后
参数参数
变化率/%旅客选择概率变化率/% 初值敏感指数/% 转移航司 既有航司 转移航司 既有航司 $ \varphi $ 0.5 0.75 50 −2.66 6.86 −5.32 13.72 $ \rho $ 0.5 0.25 −50 −1.16 3.14 2.32 −6.28 $ {\theta ^k} $ 25 50 100 −0.60 −1.01 −0.60 −1.01 $ \alpha $ 0.5 0.75 50 0 0 0 0
下载: 导出CSV
表 5 下层博弈模型初值设置
Table 5. Initial value settings for lower level game models
$ \varphi $ $ \rho $ $ {\theta ^k} $ $ \alpha $ 0.5 0.5 25 0.5
下载: 导出CSV
表 6 渗流旅客转移成本参数
Table 6. Passenger transfer cost parameters
渗流路线 城际出行
成本/元城际出行
时间/min城内出行
成本/元城内出行
时间/min时间成本/
（元·h−1）北京—天津 20～180 30～60 60 90 60 北京—石家庄 40～230 60～130 40 70 60
下载: 导出CSV
-
[1] SU M, LUAN W X, YUAN L Y, et al. Sustainability development of high-speed rail and airline: understanding passengers’ preferences: a case study of the Beijing–Shanghai corridor[J]. Sustainability, 2019, 11(5): 1352. doi: 10.3390/su11051352 [2] TERAJI Y, MORIMOTO Y. Price competition of airports and its effect on the airline network[J]. Economics of Transportation, 2014, 3(1): 45-57. doi: 10.1016/j.ecotra.2014.03.001 [3] DOBRUSZKES F, GIVONI M, VOWLES T. Hello major airports, goodbye regional airports? recent changes in European and US low-cost airline airport choice[J]. Journal of Air Transport Management, 2017, 59: 50-62. [4] 周蔷, 王忠群, 龚本刚. 基于航线网络的定价、超售与舱位控制策略研究[J]. 兰州大学学报(自然科学版), 2016, 52(1): 126-134.ZHOU Q, WANG Z Q, GONG B G. Strategy research on the pricing, overbooking and cabin inventory control of airline network[J]. Journal of Lanzhou University (Natural Sciences), 2016, 52(1): 126-134(in Chinese). [5] PENG I C, LU H A. Coopetition effects among global airline alliances for selected Asian airports[J]. Journal of Air Transport Management, 2022, 101: 102193. doi: 10.1016/j.jairtraman.2022.102193 [6] 骆嘉琪, 匡海波, 冯涛, 等. 基于两阶段博弈模型的高铁民航竞合关系研究[J]. 系统工程理论与实践, 2019, 39(1): 150-164. doi: 10.12011/1000-6788-2018-0154-15LUO J Q, KUANG H B, FENG T, et al. Research on the co-opetition between high speed rail and civil aviation based on two stage game model[J]. Systems Engineering-Theory & Practice, 2019, 39(1): 150-164(in Chinese). doi: 10.12011/1000-6788-2018-0154-15 [7] KIM A M, RYERSON M S. A long drive: Interregional airport passenger “leakage” in the U. S[J]. Tourism Management, 2018, 65: 237-244. doi: 10.1016/j.tourman.2017.10.012 [8] LIAO W, CAO X S, LI S C. Competition and sustainability development of a multi-airport region: a case study of the Guangdong-Hong Kong-Macao Greater Bay Area[J]. Sustainability, 2019, 11(10): 2958. doi: 10.3390/su11102958 [9] 卞骞, 宋丽英, 毛保华, 等. 基于市场进入博弈的高速铁路与航空竞争分析[J]. 交通运输系统工程与信息, 2019, 19(5): 20-27.BIAN Q, SONG L Y, MAO B H, et al. High speed rail and air transport competition: a market-entry game approach[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(5): 20-27(in Chinese). [10] YANG C W, LU J L, HSU C Y. Modeling joint airport and route choice behavior for international and metropolitan airports[J]. Journal of Air Transport Management, 2014, 39: 89-95. doi: 10.1016/j.jairtraman.2014.05.001 [11] MINATO N, MORIMOTO R. Designing the commercial sustainability of unprofitable regional airports using system dynamics analysis[J]. Research in Transportation Business & Management, 2011, 1(1): 80-90. [12] HOU M, WANG K, YANG H J. Hub airport slot re-allocation and subsidy policy to speed up air traffic recovery amid COVID-19 pandemic-case on the Chinese airline market[J]. Journal of Air Transport Management, 2021, 93: 102047. doi: 10.1016/j.jairtraman.2021.102047 [13] 陈欣, 张珍, 邱瑞, 等. 基于动态博弈的补贴模式对机场群航线网络结构的影响研究[J]. 四川大学学报(自然科学版), 2022, 59(5): 201-207.CHEN X, ZHANG Z, QIU R, et al. Research on the impact of subsidization on the airline networks of multi-airport systems based on dynamic game theory[J]. Journal of Sichuan University (Natural Science Edition), 2022, 59(5): 201-207(in Chinese). [14] 张珍. 基于博弈论的机场群管理模式和航线网络选择策略研究[D]. 南京: 南京财经大学, 2023.ZHANG Z. Research on airport group management mode and route network selection strategy based on game theory[D]. Nanjing: Nanjing University of Finance & Economics, 2023(in Chinese). [15] 魏夕凯, 马本. 农村生活垃圾分类治理的奖惩激励机制: 基于复杂网络演化博弈模型[J]. 中国环境科学, 2022, 42(8): 3822-3831. doi: 10.3969/j.issn.1000-6923.2022.08.040WEI X K, MA B. Reward and punishment incentive mechanism of domestic waste classification in rural China: based on complex network evolutionary game model[J]. China Environmental Science, 2022, 42(8): 3822-3831(in Chinese). doi: 10.3969/j.issn.1000-6923.2022.08.040 -
下载:
点击查看大图
计量
- 文章访问数: 115
- HTML全文浏览量: 28
- PDF下载量: 0
- 被引次数: 0
