Multi-stage trajectory planning method for hazard zone avoidance under uncertainty based on neural networks
-
摘要:
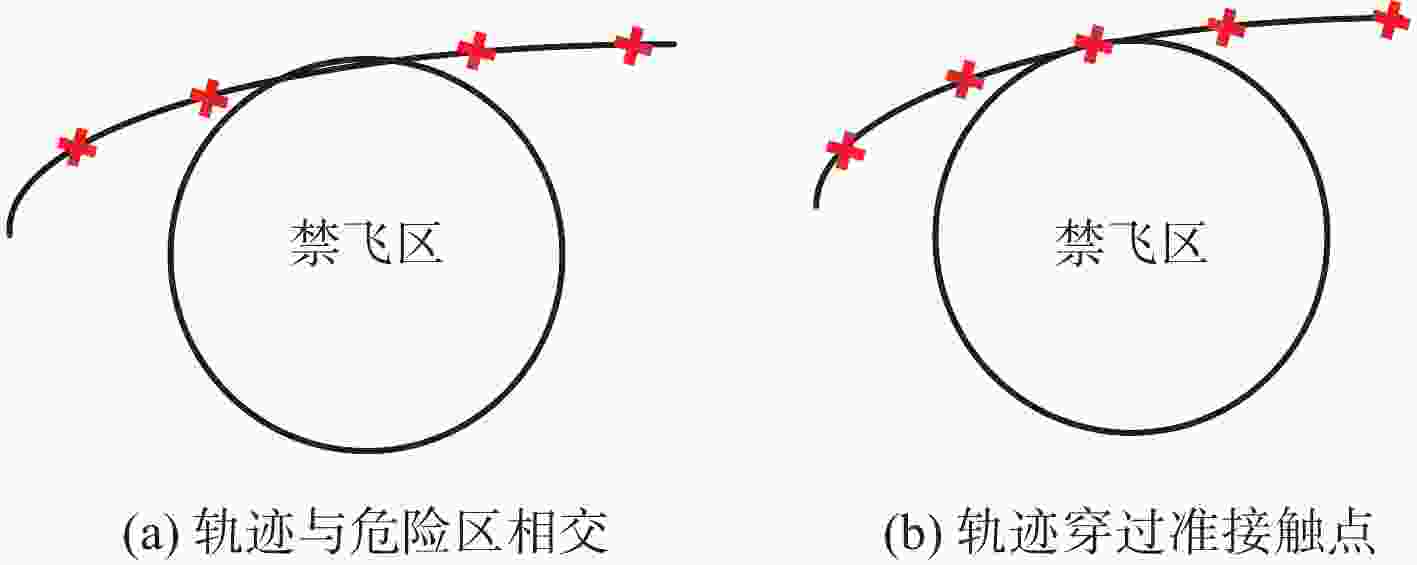
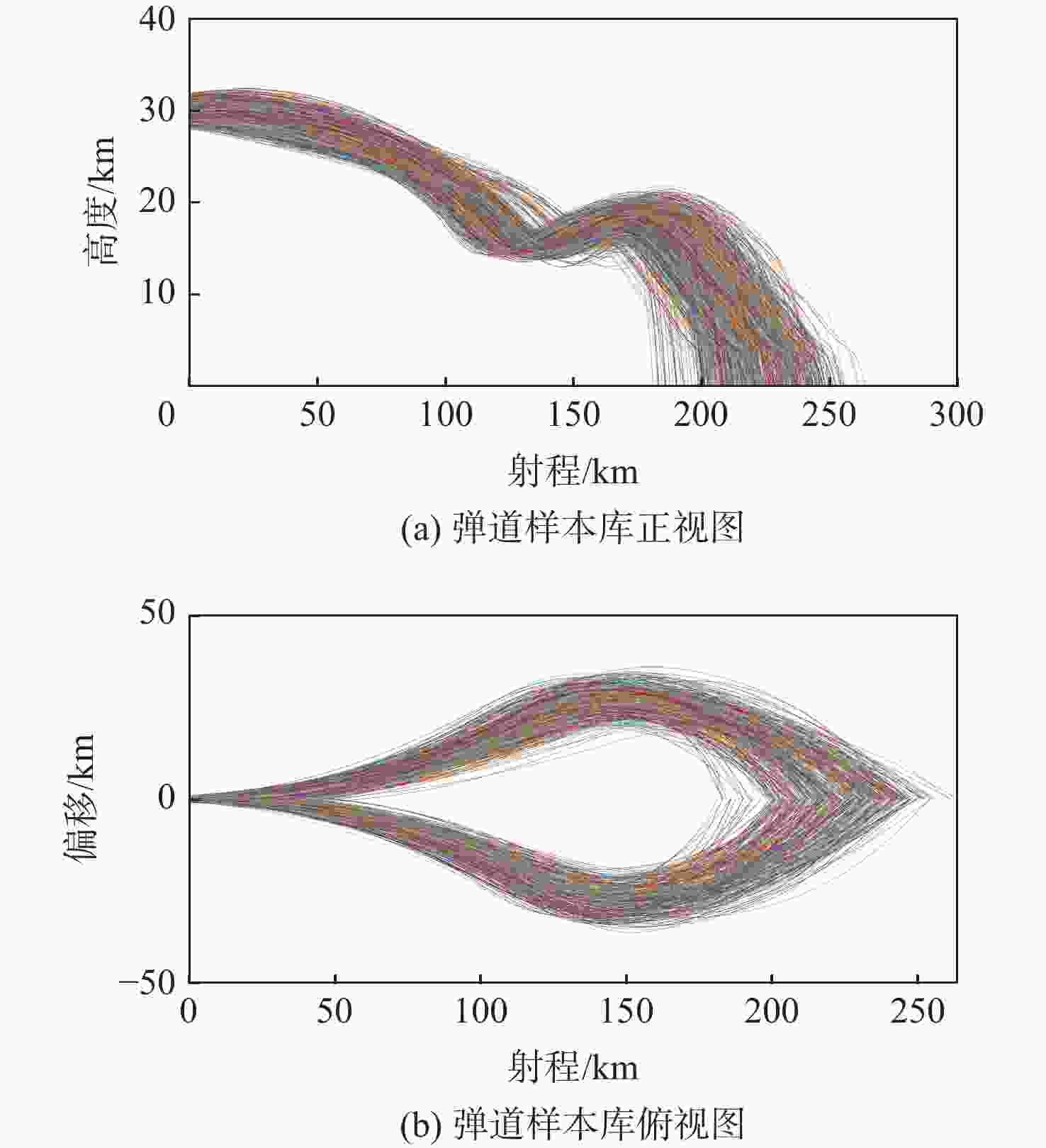
基于最优控制的弹道规划方法可以最大程度地发挥出超远程滑翔制导炮弹的飞行能力，然而在面对不确定的战场环境时，这种数值方法耗时、不易收敛的缺点导致其难以在线应用。针对这一问题，提出一种深度神经网络弹道规划方法，利用深度神经网络的非线性映射能力近似伪谱法计算模型以减少弹载计算机的运算负荷。根据弹体和环境的多种随机状态，在3维空间内以多阶段高斯伪谱法(MGPM)基于连续性条件将准接触点连接起来，形成满足路径约束的射程最优弹道样本数据库；以最优弹道数据样本库为基础，深度神经网络离线学习弹体在不同状态下的最优动作，以此映射出最优弹道规划计算模型。仿真结果表明：所提方法可以在随机状态下快速生成近似最优轨迹，具有良好的实时性和鲁棒性，可适用于解决在线弹道规划问题。
Abstract:The trajectory planning method based on optimal control can maximize the flight capability of ultra-long-range glide-guided projectiles. However, when faced with uncertain battlefield conditions, this numerical method, which is time-consuming and prone to poor convergence, makes online applications difficult. To address this issue, a deep neural network-based trajectory planning method was proposed. This method utilized the non-linear mapping ability of deep neural networks to approximate the pseudospectral method computation model, reducing the computational load on the onboard computer of the projectile. The implementation of the method was primarily divided into two steps. The first step connected pre-contact points in three-dimensional space based on continuity conditions, considering various random states of the projectile and environment, using the multi-stage Gaussian pseudospectral method (MGPM), forming a range-optimal trajectory sample database that satisfies path constraints. The second step involved mapping out the optimal trajectory planning model by having the deep neural network learn the optimal actions of the projectile under different states offline, based on the optimal trajectory data sample library. Simulation results show that the proposed method can quickly generate near-optimal trajectories under random, demonstrating good real-time performance and robustness, making it suitable for solving online trajectory planning problems.
-
图 5 在不同学习率下的DNN训练损失变化
Figure 5. Variation of DNN training loss under different learning rates
表 1 控制约束参数
Table 1. Control constraint parameters
参数 数值 $[{\alpha _{\min }},{\alpha _{\max }}]/(^\circ )$ [0,12] $[{\beta _{\min }},{\beta _{\max }}]/(^\circ )$ [−12,12] 
下载: 导出CSV
表 2 初始状态参数
Table 2. Initial state parameters
参数 数值 $v/({\text{m}} \cdot {{\text{s}}^{{{ - 1}}}})$ [ 1450 ,1550 ]$\theta /(^\circ )$ [−3,3] $ {\psi _{\text{v}}}/(^\circ ) $ [−3,3] $y/{\text{km}}$ [28,32] ${\textit{z}}/{\text{km}}$ [−1,1] ${v_{\text{f}}}/\left( {{\text{m}} \cdot {{\text{s}}^{{{ - 1}}}}} \right)$ [300,350]
下载: 导出CSV
表 3 危险区状态参数
Table 3. Danger zone status parameters
参数 数值 $x_{\mathrm{d}}^1/{\text{km}}$ [100,130] $x_{\mathrm{d}}^2/{\text{km}}$ [130,160] ${\textit{z}}_{\mathrm{d}}^1/{\text{km}}$ [−10,10] ${\textit{z}}_{\mathrm{d}}^2/{\text{km}}$ [−10,10] $r_{\mathrm{d}}^1/{\text{km}}$ [30,40] $r_{\mathrm{d}}^2/{\text{km}}$ [20,30]
下载: 导出CSV
表 4 RMSE最优网络性能
Table 4. Optimal network performance based on RMSE
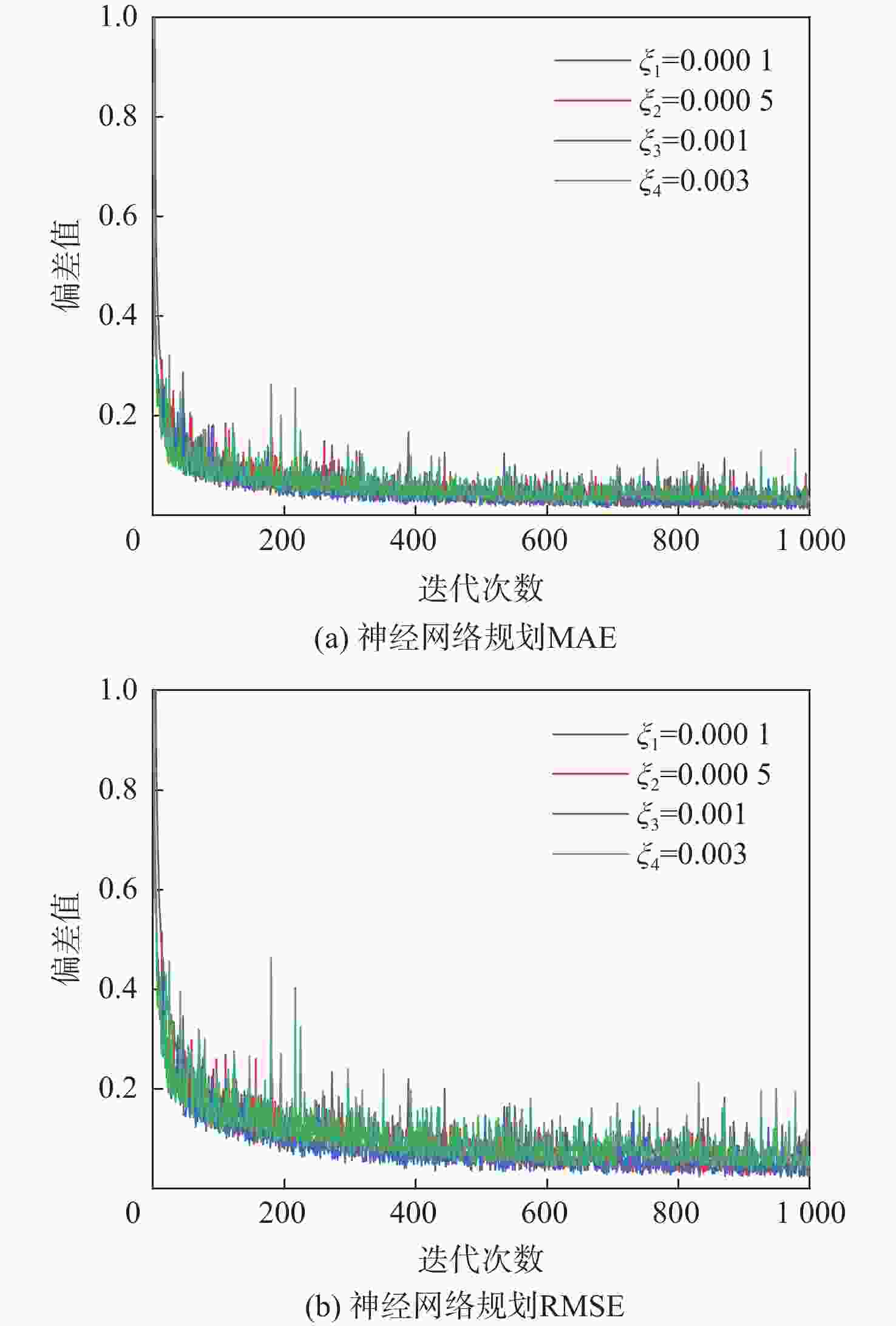
学习率$ {\xi } $ RMSE 0.0001 0.0536 0.0005 0.0320 0.001 0.0265 0.003 0.0585
下载: 导出CSV
表 5 起始状态参数和战场环境参数设置
Table 5. Settings of starting state parameters and battlefield environment parameters
参数设置 数值 高度位置y/m 30000 偏移位置z/m 0 起始速度v/(m·s−1) 1500 起始弹道倾角$\theta /(^\circ )$ 0 起始弹道偏角${\psi _v}/(^\circ )$ 0 落速约束${v_{\text{f}}}/\left( {{\text{m}} \cdot {{\text{s}}^{{\text{ - 1}}}}} \right)$ 330 危险区1位置$ \left( {x_{\text{d}}^{\text{1}},{\textit{z}}_{\text{d}}^{\text{1}},r_{\text{d}}^{\text{1}}} \right)/{\text{km}} $ (110,10,30) 危险区2位置$\left( {x_{\text{d}}^{\text{2}},{\textit{z}}_{\text{d}}^{\text{2}},r_{\text{d}}^{\text{2}}} \right)/{\text{km}}$ (160,−5,20)
下载: 导出CSV
表 6 DNN和MGPM在每阶段结束后的数值差
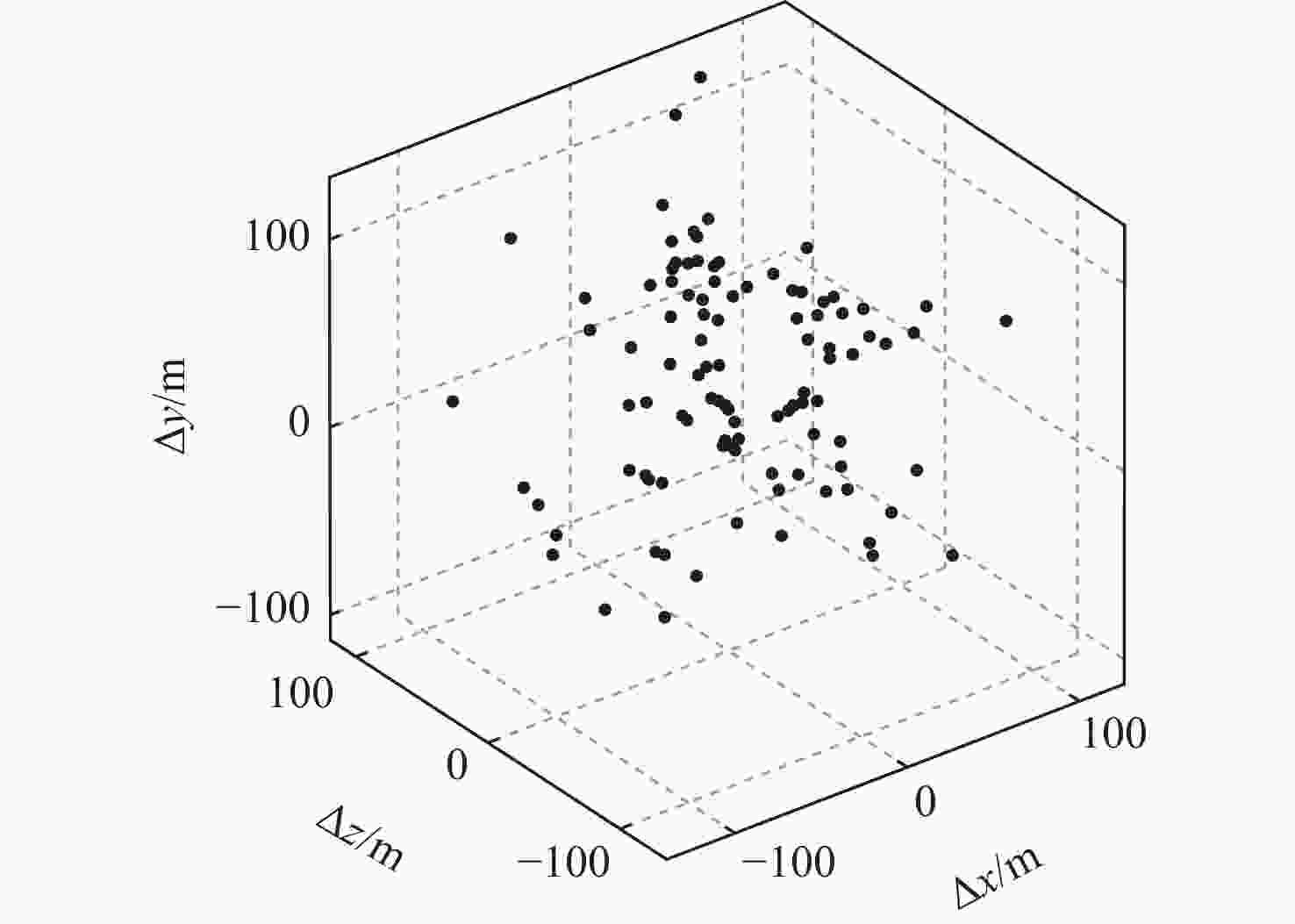
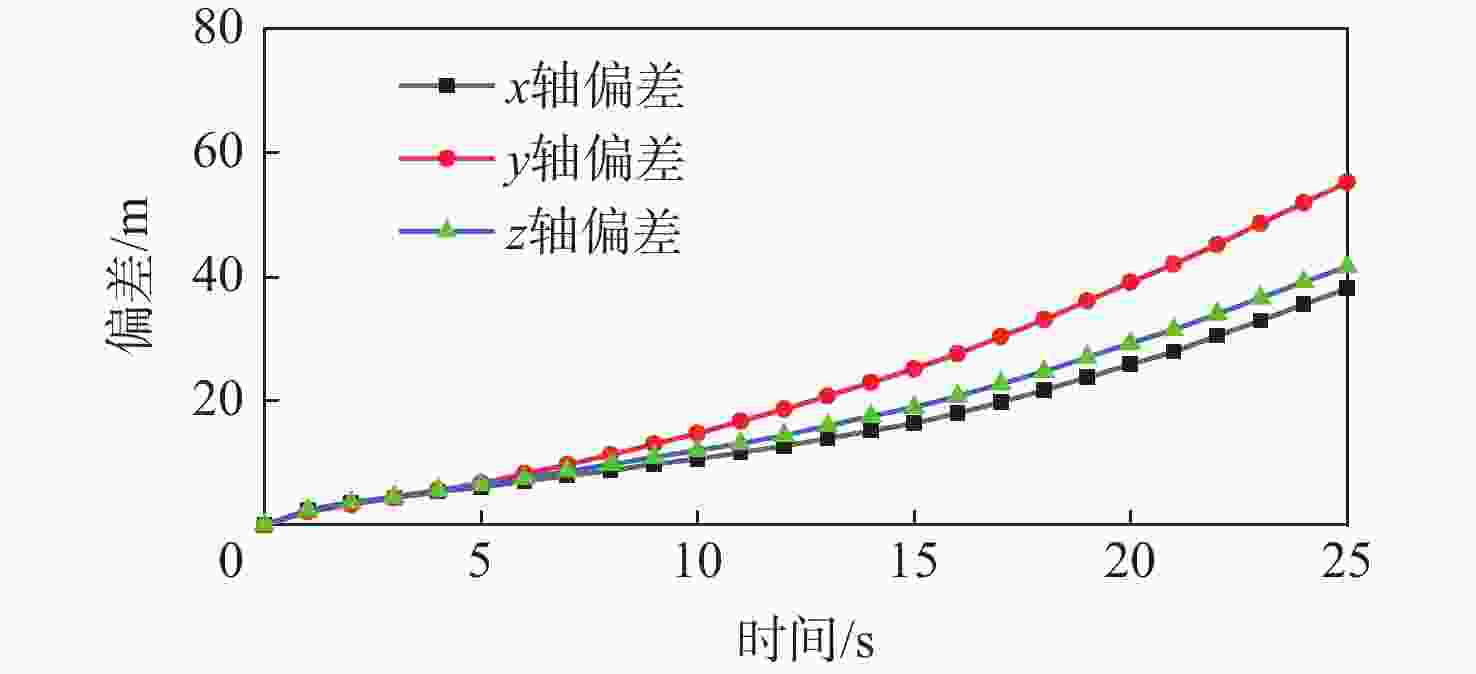
Table 6. Difference between DNN and MGPM at the end of each stage
阶段 $\Delta x/{\mathrm{m}}$ $\Delta y/{\mathrm{m}}$ $\Delta {\textit{z}}/{\mathrm{m}}$ $\Delta \theta $/(°) $\Delta {\psi _v} $/(°) $\Delta v/({\mathrm{m}} \cdot {{\mathrm{s}}^{ - 1}})$ Phase 1 83.28 43.89 56.79 0.10 0.00 1.77 Phase 2 −5.53 69.58 24.09 0.15 0.08 −3.52 Phase 3 18.17 91.55 63.50 0.19 −0.14 −2.03 Phase 4 0.00 53.03 63.43 0.08 −0.23 −0.42 Phase 5 −60.09 4.54 −43.20 0.51 −0.26 −10.69 Phase 6 −57.86 24.07 −10.35 0.03 −0.21 −7.14 Phase 7 −17.65 15.84 12.28 −0.14 −0.27 −1.98 Phase 8 9.15 −1.89 65.98 −0.16 −0.73 1.83 Phase 9 −33.29 28.03 71.96 −0.03 1.20 0.59 Phase 10 −39.32 −28.61 125.19 −0.02 −1.86 −1.36 Phase 11 −113.22 −36.39 −3.32 1.36 −0.87 −5.64 Phase 12 −37.82 −133.62 42.23 −7.35 −0.88 9.06 Phase 13 35.80 0.00 −26.37 −0.37 0.90 −3.85
下载: 导出CSV
-
[1] 沈林成, 陈璟, 王楠. 飞行器任务规划技术综述[J]. 航空学报, 2014, 35(3): 593-606.SHEN L C, CHEN J, WANG N. Overview of air vehicle mission planning techniques[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 593-606 (in Chinese). [2] BETTS J T. Survey of numerical methods for trajectory optimization[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(2): 193-207. doi: 10.2514/2.4231 [3] SHIRAZI A, CEBERIO J, LOZANO J A. Spacecraft trajectory optimization: a review of models, objectives, approaches and solutions[J]. Progress in Aerospace Sciences, 2018, 102: 76-98. doi: 10.1016/j.paerosci.2018.07.007 [4] 张远龙, 谢愈. 滑翔飞行器弹道规划与制导方法综述[J]. 航空学报, 2020, 41(1): 023377.ZHANG Y L, XIE Y. Review of trajectory planning and guidance methods for gliding vehicles[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(1): 023377 (in Chinese). [5] 黄长强, 国海峰, 丁达理. 高超声速滑翔飞行器轨迹优化与制导综述[J]. 宇航学报, 2014, 35(4): 369-379.HUANG C Q, GUO H F, DING D L. A survey of trajectory optimization and guidance for hypersonic gliding vehicle[J]. Journal of Astronautics, 2014, 35(4): 369-379 (in Chinese). [6] ZHAO J, ZHOU R. Reentry trajectory optimization for hypersonic vehicle satisfying complex constraints[J]. Chinese Journal of Aeronautics, 2013, 26(6): 1544-1553. doi: 10.1016/j.cja.2013.10.009 [7] 刘超越, 张成. 基于高斯伪谱法的二级助推战术火箭多阶段轨迹优化[J]. 兵工学报, 2019, 40(2): 292-302.LIU C Y, ZHANG C. Multi-stage trajectory optimization of tactical two-stage booster rocket based on Gauss pseudospectral method[J]. Acta Armamentarii, 2019, 40(2): 292-302 (in Chinese). [8] SU Y, DAI Y, LIU Y. A hybrid hyper-heuristic whale optimization algorithm for reusable launch vehicle reentry trajectory optimization[J]. Aerospace Science and Technology, 2021, 119: 107200. doi: 10.1016/j.ast.2021.107200 [9] CHAI R Q, SAVVARIS A, TSOURDOS A, et al. Optimal tracking guidance for aeroassisted spacecraft reconnaissance mission based on receding horizon control[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(4): 1575-1588. doi: 10.1109/TAES.2018.2798219 [10] CONWAY B A. A survey of methods available for the numerical optimization of continuous dynamic systems[J]. Journal of Optimization Theory and Applications, 2012, 152(2): 271-306. doi: 10.1007/s10957-011-9918-z [11] 杨希祥, 李晓斌, 肖飞, 等. 智能优化算法及其在飞行器优化设计领域的应用综述[J]. 宇航学报, 2009, 30(6): 2051-2061. doi: 10.3873/j.issn.1000-1328.2009.06.001YANG X X, LI X B, XIAO F, et al. Overview of intelligent optimization algorithm and its application in flight vehicles optimization design[J]. Journal of Astronautics, 2009, 30(6): 2051-2061 (in Chinese). doi: 10.3873/j.issn.1000-1328.2009.06.001 [12] 黄旭星, 李爽, 杨彬, 等. 人工智能在航天器制导与控制中的应用综述[J]. 航空学报, 2021, 42(4): 524201.HUANG X X, LI S, YANG B, et al. Spacecraft guidance and control based on artificial intelligence: review[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(4): 524201 (in Chinese). [13] 魏毅寅, 郝明瑞, 范宇. 人工智能技术在宽域飞行器控制中的应用[J]. 宇航学报, 2023, 44(4): 530-537. doi: 10.3873/j.issn.1000-1328.2023.04.007WEI Y Y, HAO M R, FAN Y. The application of artificial intelligence technology in wide-field vehicle control[J]. Journal of Astronautics, 2023, 44(4): 530-537 (in Chinese). doi: 10.3873/j.issn.1000-1328.2023.04.007 [14] EFFATI S, PAKDAMAN M. Optimal control problem via neural networks[J]. Neural Computing and Applications, 2013, 23(7): 2093-2100. [15] SHI J L, WANG J B, SU L F, et al. A neural network warm-started indirect trajectory optimization method[J]. Aerospace, 2022, 9(8): 435. doi: 10.3390/aerospace9080435 [16] LI X, WANG L, WANG H, et al. A warm-started trajectory planner for fixed-wing unmanned aerial vehicle formation[J]. Applied Mathematical Modelling, 2023, 122: 200-219. doi: 10.1016/j.apm.2023.05.035 [17] SÁNCHEZ-SÁNCHEZ C, IZZO D. Real-time optimal control via deep neural networks: study on landing problems[J]. Journal of Guidance, Control, and Dynamics, 2018, 41(5): 1122-1135. doi: 10.2514/1.G002357 [18] CHENG L, WANG Z B, JIANG F H, et al. Fast generation of optimal asteroid landing trajectories using deep neural networks[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 56(4): 2642-2655. [19] WANG J B, MA H J, LI H X, et al. Real-time guidance for powered landing of reusable rockets via deep learning[J]. Neural Computing and Applications, 2023, 35(9): 6383-6404. doi: 10.1007/s00521-022-08024-4 [20] CHAI R Q, TSOURDOS A, SAVVARIS A, et al. Real-time reentry trajectory planning of hypersonic vehicles: a two-step strategy incorporating fuzzy multiobjective transcription and deep neural network[J]. IEEE Transactions on Industrial Electronics, 2019, 67(8): 6904-6915. [21] DAI P, FENG D Z, FENG W H, et al. Entry trajectory optimization for hypersonic vehicles based on convex programming and neural network[J]. Aerospace Science and Technology, 2023, 137: 108259. doi: 10.1016/j.ast.2023.108259 -
下载:
点击查看大图
计量
- 文章访问数: 163
- HTML全文浏览量: 44
- PDF下载量: 4
- 被引次数: 0
