带软时间窗的多调度中心UAV安全运输线路和航迹协同规划

魏明; 孙雅茹; 孙博; 王盛杰

doi:10.13700/j.bh.1001-5965.2023.0509

带软时间窗的多调度中心UAV安全运输线路和航迹协同规划

doi: 10.13700/j.bh.1001-5965.2023.0509

魏明^{1, 2, ,},
孙雅茹¹,
孙博¹,
王盛杰²

1.
中国民航大学空中交通管理学院，天津 300300
2.
中国民用航空飞行学院民航飞行技术与飞行安全重点实验室，广汉 618300

基金项目:

民航飞行技术与飞行安全重点实验室开放基金(FZ2021KF06)；教育部人文社科项目(20YJCZH176)

详细信息

通讯作者:
E-mail：mwei@cauc.edu.cn

中图分类号: U8
计量
- 文章访问数: 499
- HTML全文浏览量: 107
- PDF下载量: 24
- 被引次数: 0
出版历程
- 收稿日期: 2023-08-04
- 录用日期: 2023-09-03
- 网络出版日期: 2024-01-08
- 整期出版日期: 2025-10-31

Cooperative planning for safe transportation routes and flight paths of UAV with multiple dispatching centers and soft time windows

WEI Ming^{1, 2
, ,},
SUN Yaru¹,
SUN Bo¹,
WANG Shengjie²

1.
School of Air Traffic Management，Civil Aviation University of China，Tianjin 300300，China
2.
Key Laboratory of Flight Techniques and Flight Safety，Civil Aviation Flight University of China，Guanghan 618300，China

Funds:

Open Fund of Key Laboratory of Flight Techniques and Flight Safety (FZ2021KF06); The Ministry of Education of Humanities and Social Science Project (20YJCZH176)

More Information

Corresponding author: E-mail：mwei@cauc.edu.cn

摘要

摘要:
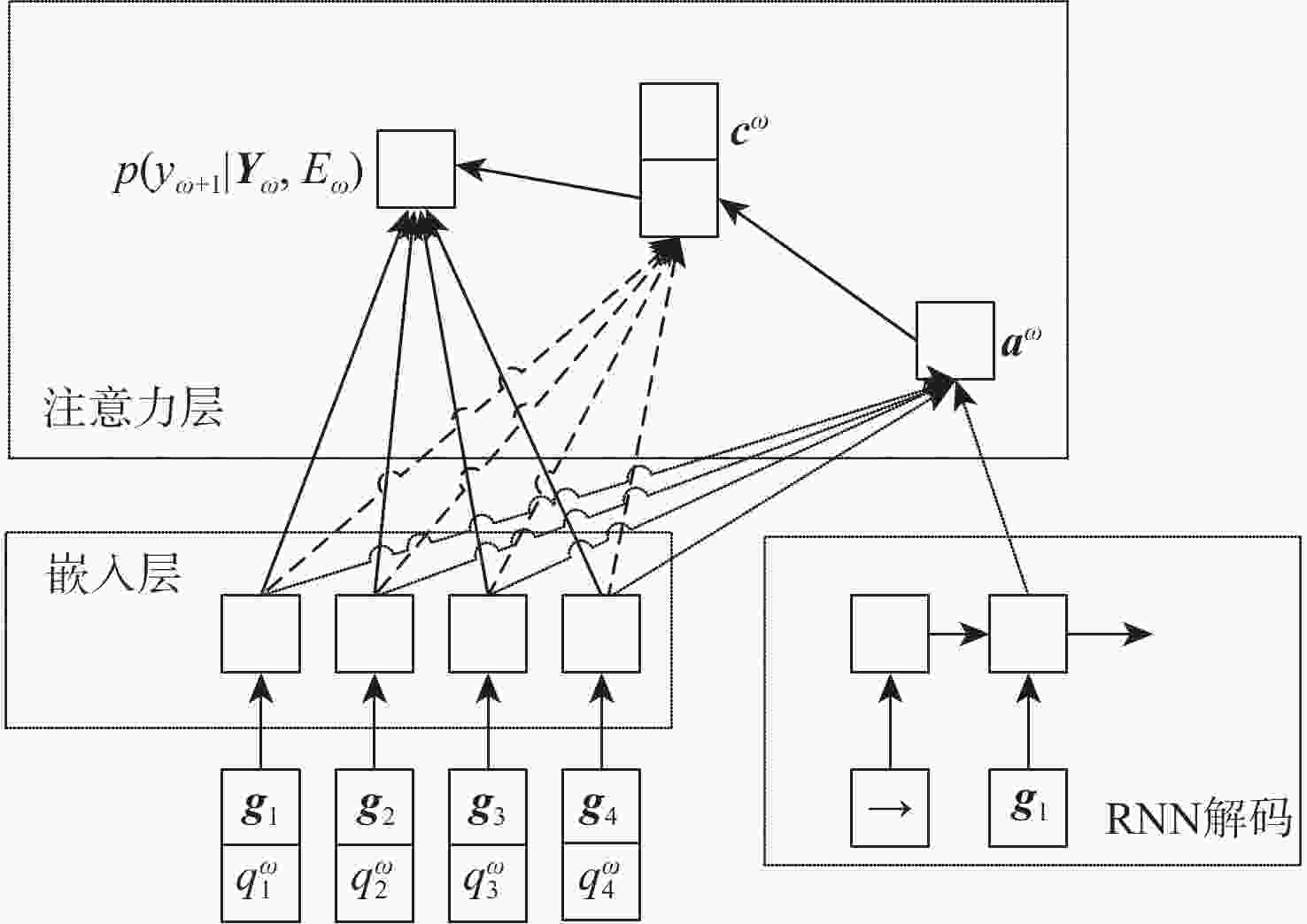
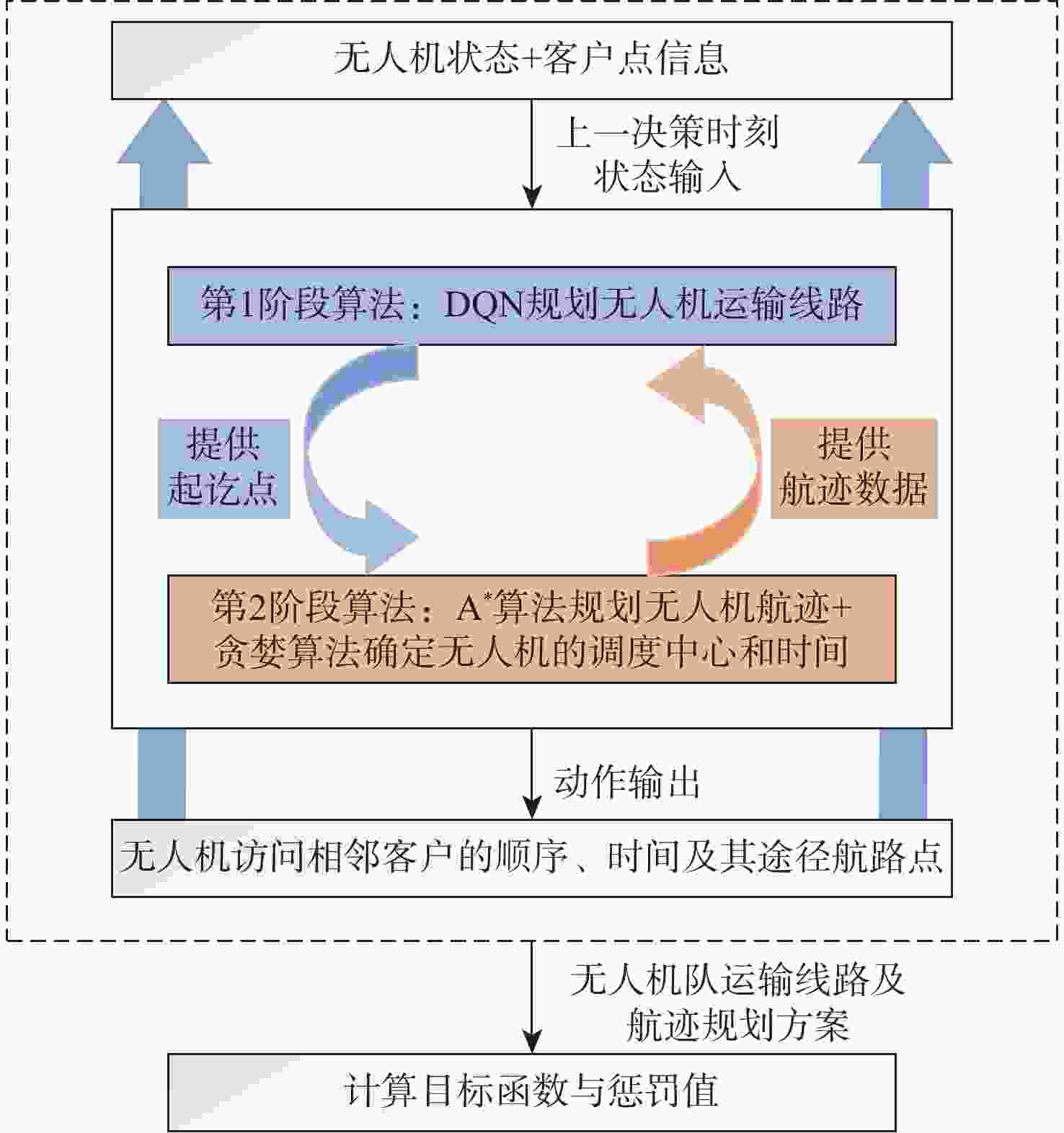
针对面向物流配送的无人机(UAV)运输线路和航迹规划问题，建立了一种协同规划双层模型。上层模型考虑客户时间窗、无人机载重、能耗和路径风险等约束因素，计算无人机的出发时间、调度中心及其访问客户的顺序和调度时间表，实现无人机调度成本最低；下层模型考虑障碍物、无线电干扰与无人机坠落代价等多重安全因素，计算无人机在任意调度中心和客户之间可行的最短飞行航迹。根据问题特征，设计求解该问题的嵌入A^*算法和贪婪策略的两阶段深度强化学习(DRL)算法。通过案例计算最佳的无人机运输线路及其航迹规划方案，分析关键参数的变化对调度结果的影响，并与遗传算法(GA)、差分进化(DE)算法及粒子群优化(PSO)算法进行对比，验证所提算法的有效性和正确性。
- 航空运输 /
- 无人机运输线路 /
- 无人机航迹 /
- 双层模型 /
- 深度强化学习 /
- A^*算法
Abstract:
A two-layer collaborative planning model is established for the problem of unmanned aerial vehicle (UAV) transportation routes and flight paths planning for logistics distribution. In the upper-level model, considering constraint factors such as customer time windows, UAV load, energy consumption, and path risk, the UAV’s departure dispatching center, access sequence, and customer arrival times were calculated to minimize UAV dispatching costs. In the lower-level model, considering multiple safety factors such as obstacles, radio interference, and UAV crash costs, the shortest feasible flight path between any dispatching center and customers was calculated. A two-stage deep reinforcement learning (DRL) algorithm, incorporating the A^* algorithm and a greedy strategy, was designed to solve the problem based on its characteristics. Finally, a case studywas presented where the optimal UAV transportation route and flight path planning scheme were calculated, and the impact of changes in key parameters on the scheduling results was analyzed. The validity and accuracy of this paper were verified by comparison with genetic algorithm (GA), differential evolution (DE) and particle swarm optimization (PSO) algorithms.
- air transport /
- unmanned aerial vehicle transportation route /
- unmanned aerial vehicle flight path /
- two-layer model /
- deep reinforcement learning /
- A^* algorithm

HTML全文

图 1 基于深度强化学习的两阶段求解框架

Figure 1. Two-stage solution framework based on deep reinforcement learning

下载: 全尺寸图片幻灯片

图 2 指针网络结构

Figure 2. Pointer network structure

下载: 全尺寸图片幻灯片

图 3 模型训练的算法流程

Figure 3. Algorithm flow for model training

下载: 全尺寸图片幻灯片

图 4 考虑障碍物分布、坠落代价和无线电干扰的配送区域GIS栅格化

Figure 4. GIS rasterization of distribution area considering obstacle distribution, crash cost, and radio interference

下载: 全尺寸图片幻灯片

图 5 基于深度强化学习算法的寻优过程曲线

Figure 5. Optimization process curve based on deep reinforcement learning algorithm

下载: 全尺寸图片幻灯片

图 6 上层模型的无人机队运输线路可视化

Figure 6. Visualization of UAV transport routes in upper-level model

下载: 全尺寸图片幻灯片

图 7 下层模型的无人机队航迹可视化

Figure 7. Visualization of UAV flight paths in lower-level model

下载: 全尺寸图片幻灯片

图 8 不同坠落代价阈值对双层模型结果的影响

Figure 8. Effect of different crash cost thresholds on results of two-layer model

下载: 全尺寸图片幻灯片

图 9 灵活和固定出发时间对双层模型结果的影响

Figure 9. Effect of flexible and fixed departure time on results of two-layer model

下载: 全尺寸图片幻灯片

图 10 单/多调度中心对双层模型结果的影响

Figure 10. Effect of single/multiple dispatch centers on results of two-layer model

下载: 全尺寸图片幻灯片

图 11 不同无线电干扰强度对双层模型结果的影响

Figure 11. Effect of different radio interference intensities on results of two-layer mode

下载: 全尺寸图片幻灯片

表 1 客户基本信息

Table 1. Customer basic information

需求点（坐标）	最早时间	最晚时间	需求量/kg
D1(0,27)	06:24	06:29	1
D2(1,12)	06:20	06:25	2
D3(1,4)	06:00	06:05	1
D4(4,22)	06:26	06:31	3
D5(5,18)	06:27	06:32	1
D6(6,17)	06:27	06:32	2
D7(7,11)	06:20	06:25	1
D8(6,2)	06:02	06:07	1
D9(9,19)	06:12	06:17	1
D10(7,2)	06:02	06:07	2
D11(10,12)	06:15	06:21	1
D12(10,23)	06:10	06:15	1
D13(12,5)	06:03	06:08	1
D14(13,9)	06:03	06:08	2
D15(14,5)	06:20	06:25	3
D16(16,13)	06:16	06:21	1
D17(17,20)	06:18	06:23	1
D18(18,17)	06:17	06:22	2
D19(21,17)	06:30	06:35	2
D20(22,21)	06:35	06:40	1
D21(23,15)	06:31	06:36	2
D22(24,21)	06:33	06:38	1
D23(25,25)	06:34	06:39	1
D24(27,7)	06:26	06:31	2
D25(27,24)	06:34	06:39	1
D26(28,13)	06:25	06:30	2
D27(29,7)	06:27	06:32	2

下载: 导出CSV

表 2 最佳调度方案

Table 2. The optimal scheduling scheme

无人机	线路及时间规划	航程/km	滞后时间/min	等待时间/min	能耗/ (kW·h)
UAV1	S1(06:05:00)—D13(06:06:06)—D14(06:07:07)—D9(06:09:37)— D16(06:14:13)—D11(06:17:20)—D15(06:19:08)—S1(06:21:30)	11.022	0	5.00	0.900
UAV2	S1(06:03:00)—D3(06:04:48)—D8(06:06:01)—D10(06:06:13)— D2(06:08:50)—D7(06:21:20)—DS1(06:30:42)	7.560	0	19.83	0.596
UAV3	S2(06:20:00)—D17(06:21:13)—D18(06:21:56)—D20(06:23:14)— D22(06:35:25)—D25(06:36:18)—D23(06:36:48)—S2(06:39:04)	6.994	0	11.78	0.534
UAV4	S2(06:13:00)—D12(06:14:13)—D1(06:16:39)—D5(06:26:18)— D6(06:27:18)—D4(06:28:31)—DS2(06:31:21)	9.891	0	8.05	0.798
UAV5	S3(06:26:00)—D27(06:27:00)—D26(06:28:21)—D24(06:29:41)— D19(06:32:17)—D21(06:32:52)—DS3(06:35:25)	9.043	0	0	0.726

下载: 导出CSV

表 3 不同订单规模的多种算法性能对比

Table 3. Performance comparison of multiple algorithms for different order sizes

客户数量	算法	运营成本/元				求解时间/s
客户数量	算法	近最优解	平均解	最差解	标准差	求解时间/s
27	DRL	10163.25	10283.63	10696.34	53.25	10.26
	GA	10589.28	15206.35	45646.75	4796.39	44.34
	DE	13087.94	27396.45	51437.46	5068.57	45.87
	PSO	11035.69	13387.29	41638.84	3678.77	900.44
50	DRL	26576.69	27492.59	28675.39	636.35	30.64
	GA	26824.57	59375.78	97305.03	11372.49	86.75
	DE	36127.49	80543.46	100837.54	15453.55	88.45
	PSO	42198.26	114385.58	189627.29	10783.89	1703.45
100	DRL	40783.58	47295.49	53652.03	982.32	42.58
	GA	54782.36	88547.57	238693.72	32981.49	148.29
	DE	62642.23	100458.28	219051.03	20682.68	209.61
	PSO	80681.56	189672.67	286319.57	26890.33	3662.82

下载: 导出CSV

参考文献(19)

[1]	DORLING K, HEINRICHS J, MESSIER G G, et al. Vehicle routing problems for drone delivery[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2017, 47(1): 70-85. doi: 10.1109/TSMC.2016.2582745
[2]	WANG X D, LIU Z Y, LI X P. Optimal delivery route planning for a fleet of heterogeneous drones: a rescheduling-based genetic algorithm approach[J]. Computers & Industrial Engineering, 2023, 179: 109179.
[3]	SONGBD, PARK K, KIM J. Persistent UAV delivery logistics: MILP formulation and efficient heuristic[J]. Computers & Industrial Engineering, 2018, 120: 418-428.
[4]	CHENG C, ADULYASAK Y, ROUSSEAU L M. Drone routing with energy function: formulation and exact algorithm[J]. Transportation Research Part B: Methodological, 2020, 139: 364-387. doi: 10.1016/j.trb.2020.06.011
[5]	张建行, 康凯, 钱骅, 等. 面向物联网的深度Q网络无人机路径规划[J]. 电子与信息学报, 2022, 44(11): 3850-3857. doi: 10.11999/JEIT210962 ZHANG J H, KANG K, QIAN H, et al. UAV trajectory planning based on deep Q-network for Internet of things[J]. Journal of Electronics & Information Technology, 2022, 44(11): 3850-3857(in Chinese). doi: 10.11999/JEIT210962
[6]	袁一帆, 吴德伟, 戴传金, 等. 基于RRT算法改进的无人机航迹规划研究[J]. 战术导弹技术, 2022(5): 126-133. YUAN Y F, WU D W, DAI C J, et al. Research on UAV’s path planning based on improved RRT algorithm[J]. Tactical Missile Technology, 2022(5): 126-133(in Chinese).
[7]	LIN N, TANG J C, LI X W, et al. A novel improved bat algorithm in UAV path planning[J]. Computers, Materials & Continua, 2019, 61(1): 323-344.
[8]	XU C, XU M, YIN C J. Optimized multi-UAV cooperative path planning under the complex confrontation environment[J]. Computer Communications, 2020, 162: 196-203. doi: 10.1016/j.comcom.2020.04.050
[9]	SHAO S K, PENG Y, HE C L, et al. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization[J]. ISA Transactions, 2020, 97: 415-430. doi: 10.1016/j.isatra.2019.08.018
[10]	ZHOU Y M, SU Y, XIE A H, et al. A newly bio-inspired path planning algorithm for autonomous obstacle avoidance of UAV[J]. Chinese Journal of Aeronautics, 2021, 34(9): 199-209. doi: 10.1016/j.cja.2020.12.018
[11]	刘光才, 马寅松, 齐福强, 等. 基于改进A^-人工势场法的城市物流无人机路径规划[J]. 飞行力学, 2022, 40(6): 16-23. LIU G C, MA Y S, QI F Q, et al. Flight path planning for urban logistics UAV based on improved A^-APF algorithm[J]. Flight Dynamics, 2022, 40(6): 16-23(in Chinese).
[12]	CHEN J C, LING F Y, ZHANG Y, et al. Coverage path planning of heterogeneous unmanned aerial vehicles based on ant colony system[J]. Swarm and Evolutionary Computation, 2022, 69: 101005. doi: 10.1016/j.swevo.2021.101005
[13]	YU X B, JIANG N J, WANG X M, et al. A hybrid algorithm based on grey wolf optimizer and differential evolution for UAV path planning[J]. Expert Systems with Applications, 2023, 215: 119327. doi: 10.1016/j.eswa.2022.119327
[14]	YU X B, LUO W G. Reinforcement learning-based multi-strategy cuckoo search algorithm for 3D UAV path planning[J]. Expert Systems with Applications, 2023, 223: 119910. doi: 10.1016/j.eswa.2023.119910
[15]	司鹏搏, 吴兵, 杨睿哲, 等. 基于多智能体深度强化学习的无人机路径规划[J]. 北京工业大学学报, 2023, 49(4): 449-458. doi: 10.11936/bjutxb2022080007 SI P B, WU B, YANG R Z, et al. UAV path planning based on multi-agent deep reinforcement learning[J]. Journal of Beijing University of Technology, 2023, 49(4): 449-458(in Chinese). doi: 10.11936/bjutxb2022080007
[16]	LIU X X, SU Y Z, WU Y, et al. Multi-conflict-based optimal algorithm for multi-UAV cooperative path planning[J]. Drones, 2023, 7(3): 217. doi: 10.3390/drones7030217
[17]	韩鹏, 赵嶷飞. 基于飞行环境建模的UAV地面撞击风险研究[J]. 中国安全科学学报, 2020, 30(1): 142-147. HAN P, ZHAO Y F. Study on ground impact risk of UAV based on flight environment[J]. China Safety Science Journal, 2020, 30(1): 142-147(in Chinese).
[18]	NAZARI M, OROOJLOOY A, SNYDER L, et al. Deep reinforcement learning for solving the vehicle routing problem[C]//Proceedings of the 32nd International Conference on Neural Information Processing Systems. New York: ACM, 2018: 9861-9871.
[19]	KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. (2017-01-30)[2023-08-01]. http://arxiv.org/abs/1412.6980.